画像 π/2 graph 150327

How do you sketch a graph of #h(x)=5frac{1}{2} \sec 4x# over the interval #0,2pi#?Tangent graph is not like a sine and cosine curve This graph looks like discontinue curve because for certain values tangent is not defined tan x = sin x / cos x For some values of x, cos x has value 0 For example, x = π/2 and x = 3π/2 When this happens, we have 0 in the denominator of the fraction and this means it is undefinedOn (− π 2, π 2), (− π 2, π 2), the graph will come up from the left asymptote at x = − π 2, x = − π 2, cross through the origin, and continue to increase as it

Qn9yfzh Yttpwm

π/2 graph

π/2 graph-Plot the graph of the inverse function of tangent, tan ⁡ − 1 θ, \tan^{1} \theta, tan − 1 θ, and describe the behavior of the asymptotes of this graph Since the inverse function is obtained by reflecting the graph about the line y = x y=x y = x , the vertical asymptotes of the tangent function become horizontal asymptotes of theAdd π 2 π 2 to both sides of the equation x = π 2 π 2 x = − π 2 π 2 Add π 2 − π 2 and π 2 π 2 x = 0 x = 0 x = 0 x = 0 Set the inside of the secant function x π 2 x − π 2 equal to 3 π 2 3 π 2 x π 2 = 3 π 2 x − π 2 = 3 π 2 Move all terms not containing x x to the right side of the equation

Webpage Of Dr Tom Cuchta

11/7/ · In this article, we will learn about graphs and nature of various inverse functions Inverse of Sine Function, y = sin1 (x) sin1 (x) is the inverse function of sin(x) Its domain is −1, 1 and its range is π/2, π/2The graph of y = tan ⁡(x − π / 2) compared to the graph of y = tan ⁡x hasGraph y = 1/3 cos(xπ/2) YouTube Graph trig function;

We're asked to graph the function y = 2sin(x) on the interval the closed interval so it includes the endpoints 2π to 2π So to do this I'm going to graph the function y = sin(x) and then think about how it's changed by the 2 and the negative in front of the x over here So let's look at the sine of x first So let me draw our xaxis let me draw the yaxis pretty straight forward and we careYou can use the transformed graph of the sine function to determine where the cosecant graph is positive and negative Because the graph of the transformed sine function is positive in between π/2 and π, the cosecant graph is positive as well andAmplitude, Period, Phase Shift and Frequency Some functions (like Sine and Cosine) repeat forever and are called Periodic Functions The Period goes from one peak to the next (or from any point to the next matching point) The Amplitude is the height from the center line to the peak (or to the trough) Or we can measure the height from highest to lowest points and divide that by 2

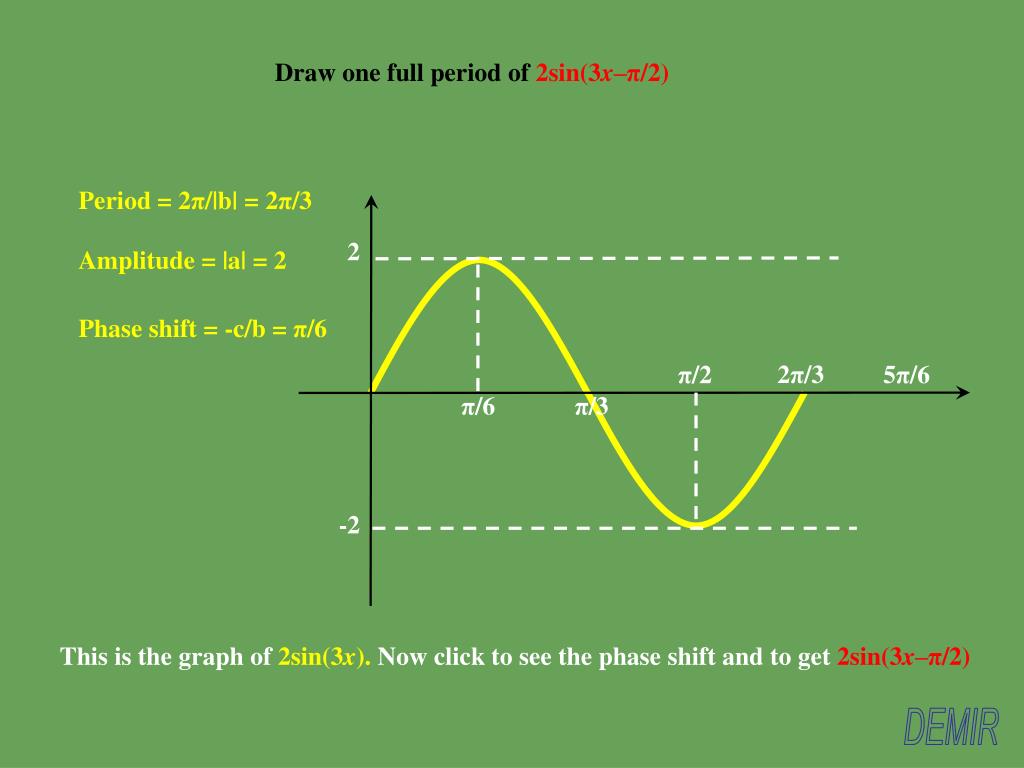
Period =2π/b = 2π/π = 2 phase shift=c/b=1/π= 1/314 = So the graph will shift to right side by units If we draw a secant curve with no shifts then the (x,y)coordinates are (0,1), (1,1) and (2,1) After shifting the coordinates will be (0 ,1), (,1) and (,1)Y coordinate of the point to graph, first locate the point p on the unit circle that corresponds to the angle θ given by the xcoordinate Then, use the ycoordinate of the point p as the y value of the point to graph To draw the graph of one period of sine or y = sin x, label the xaxis with the values 0π, π 2, π,3π 2, and 2π7/3/07 · I don't know how you'll handle the yoffset ### (which is in fact quite small compared to its probable error) or the combination of probable errors, but since T^2 = 4 π^2 L / g, the slope of your graph should be 4 π^2 / g Since that slope is / , the value alone would imply that

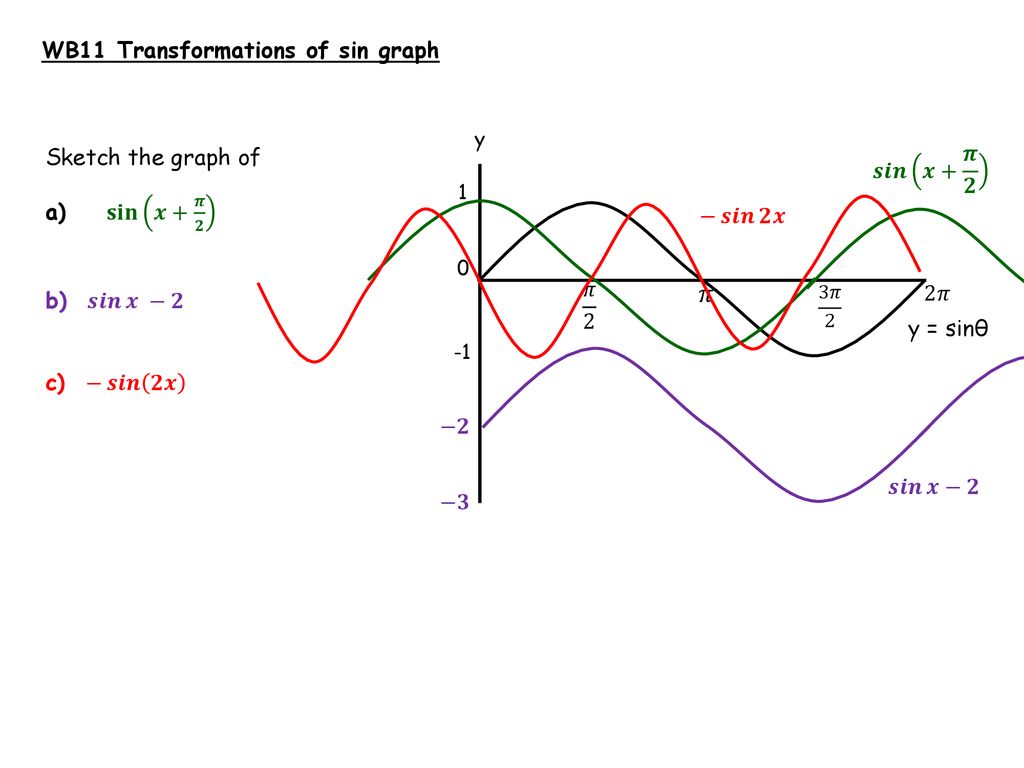
Trig Graphs And Equations Ppt Download

Ppt X Intercepts Powerpoint Presentation Free Download Id

Graph, Domain and Range of arcsin(x) In what follows, arcsin(x) is the inverse function of f(x) = sin(x) for π/2 ≤ x ≤ π/2 The domain of y = arcsin(x) is the range of f(x) = sin(x) for π/2 ≤ x ≤ π/2 and is given by the interval 1 , 1 The range of arcsin(x) is the domain of f which is given by the interval π/2 , π/24/15/18 · So the (initial) graph shown is from `pi/2` to `(7pi)/2` The vertical dashed lines are the asymptotes The pink triangle that appears when you start the animation has base length = 1 The height of that triangle is the tan ratio of the current angle You may notice the hypotenuse of the triangle is almost vertical when the graph goes off to ±∞Learn how to graph a sine function To graph a sine function, we first determine the amplitude (the maximum point on the graph), the period (the distance/tim

18 Find The Cartesian Equation Of The Curve From The Parametric Equations X Tan 2 Theta And Y Sec Theta Where Pi 2 Theta Pi 2 Then Sketch It Width Indication Of

How Can One Easier Create Nice X Axis Ticks I E Pi 2 Pi 3pi 2 In Ggplot2 Stack Overflow

DISCUSS Sinusoidal Curves The graph of y = sin x is the same as the graph of y = cos x shifted to the right π/2 units So the sine curve y = sin x is also at the same time a cosine curve y = cos ( x − π 2 ) In fact, any sine curve is also a cosine curve with a different horizontal shift, and any cosine curve is also a sine curveGraphs of functions with different amplitudes and periodsπ = 2 Step 2 Graph asymptotes of g Because the asymptotes of g occur when 1 — sin 2 πx = 0, graph x = 0, x = 1, and x = 2 Step 3 Plot points on g, such as ( — 1 2 1 — 2) and ( 3— , 2 − 1 — 2) Then use the asymptotes to sketch the curve The graph of g is a vertical shrink by a factor of 1 — and a horizontal shrink by 2

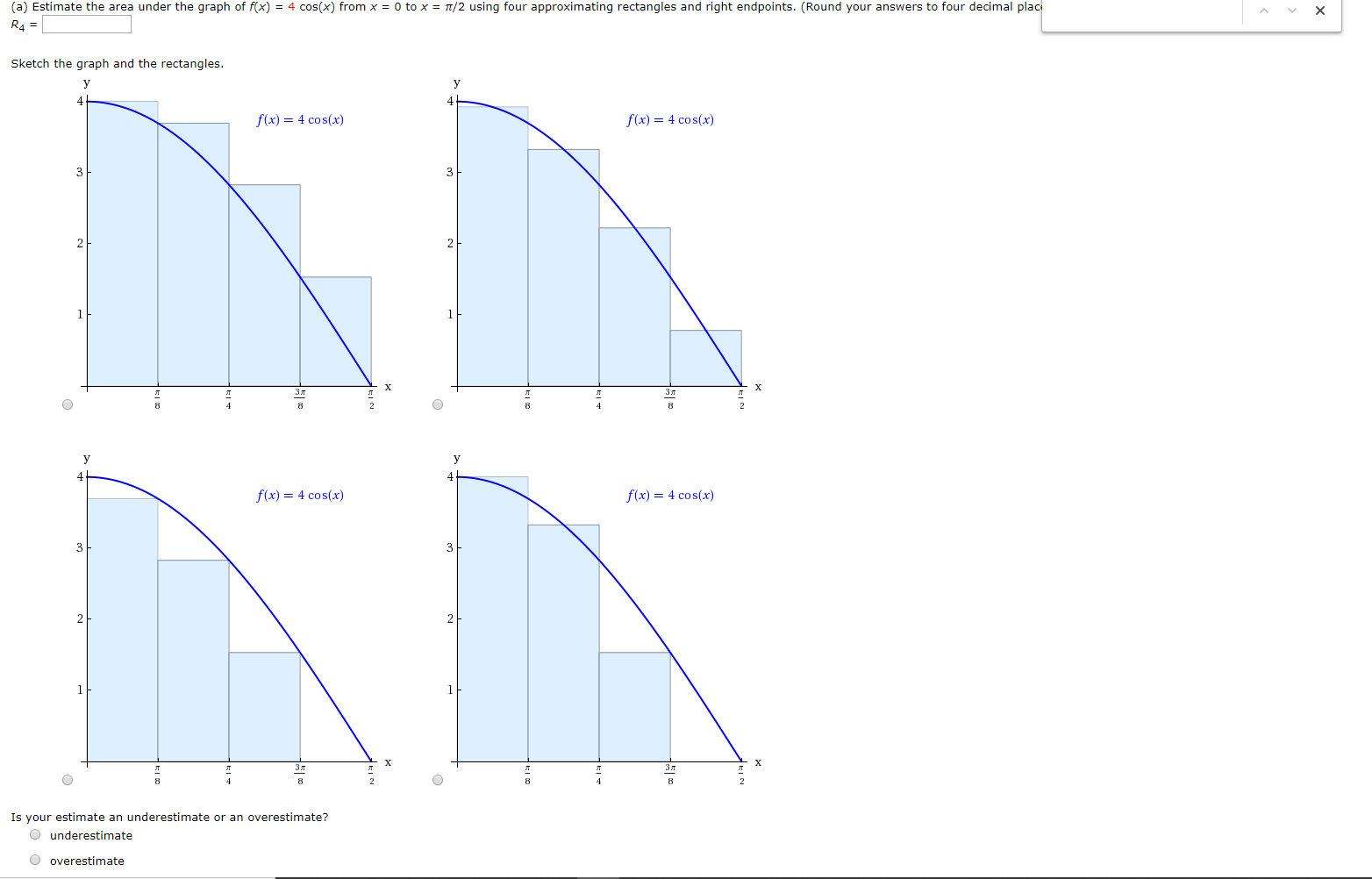
Solved A Estimate The Area Under The Graph Of F X 4 Chegg Com

Kinematics Of A Stewart Platform

Free tangent line calculator find the equation of the tangent line given a point or the intercept stepbystepWhat is the amplitude, period and frequency for the function #y=1\frac{1}{3} \cot 2x#?Here is the graph of y = sin x The height of the curve at every point is the line value of the sine In the language of functions, y = sin x is an odd function It is symmetrical with respect to the origin sin (−x) = −sin x y = cos x is an even function The independent variable x is the radian measure x may be any real number We may imagine the unit circle rolled out, in both

Aim What Are The Graphs Of Tangent Function And Reciprocal Functions Ppt Download

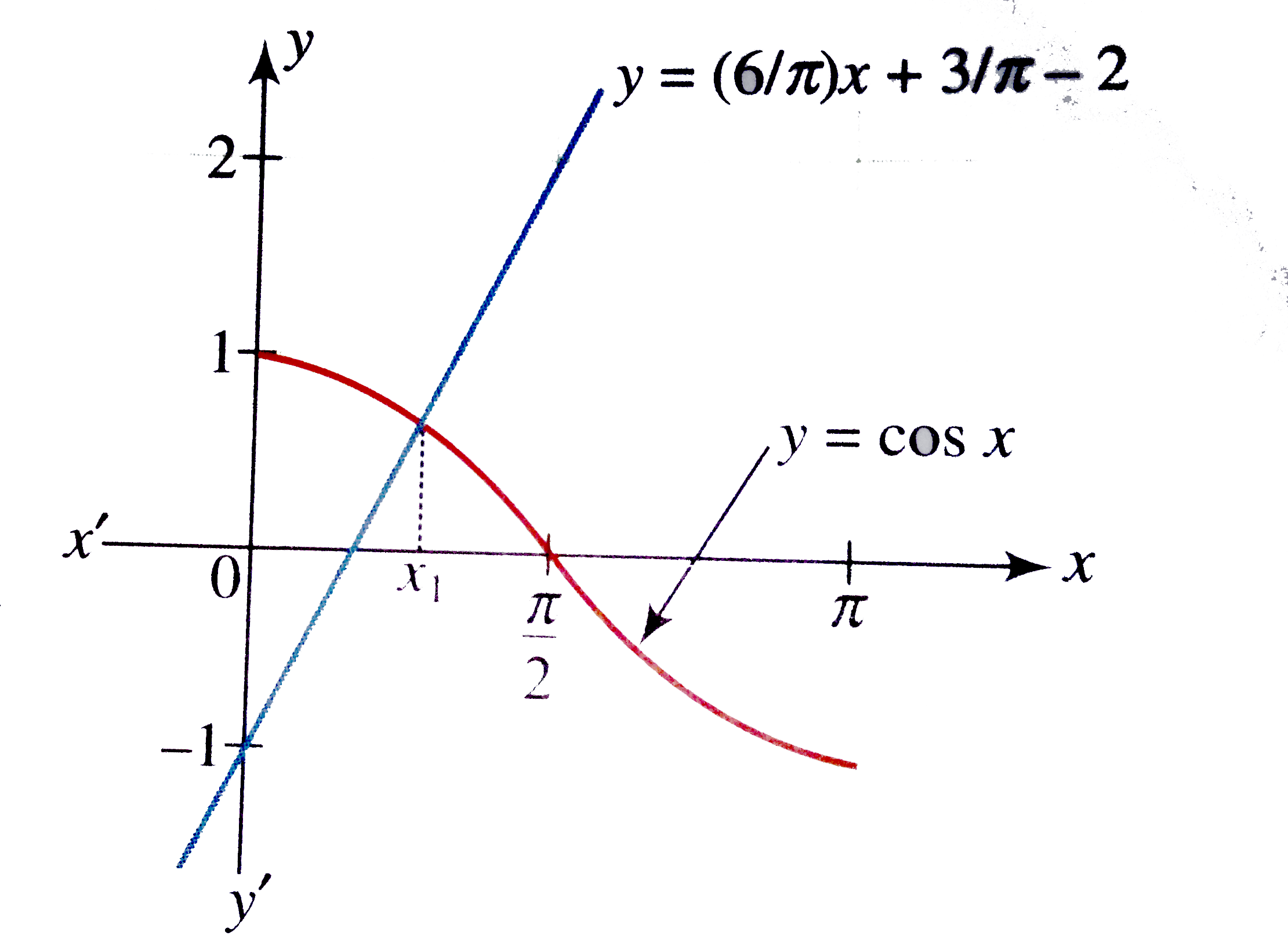
Prove That Sinx 2xgeq 3x X 1 Pi X In 0 Pi 2 Justify T

Graph of r = 2a cos θ Let's get some more practice in graphing and polar coordinates We just found π 2 ≤θ π thearea enclosed by curve r= 2acosθfor − 2 What happens when θ doesn't lie in this range?3— π 2, −1 ) The graph of g is a horizontal stretch by a factor of 2 of the graph of f MMonitoring Progressonitoring Progress Help in English and Spanish at BigIdeasMathcom Graph one period of the function Describe the graph of g as a transformation of(1 point) (a) Graph r = 1/(4 cos θ) forπ/2 < θ < π/2 and r1 Then write an iterated integral in polar coordinates representing the area inside the curve r1 and to the right of r

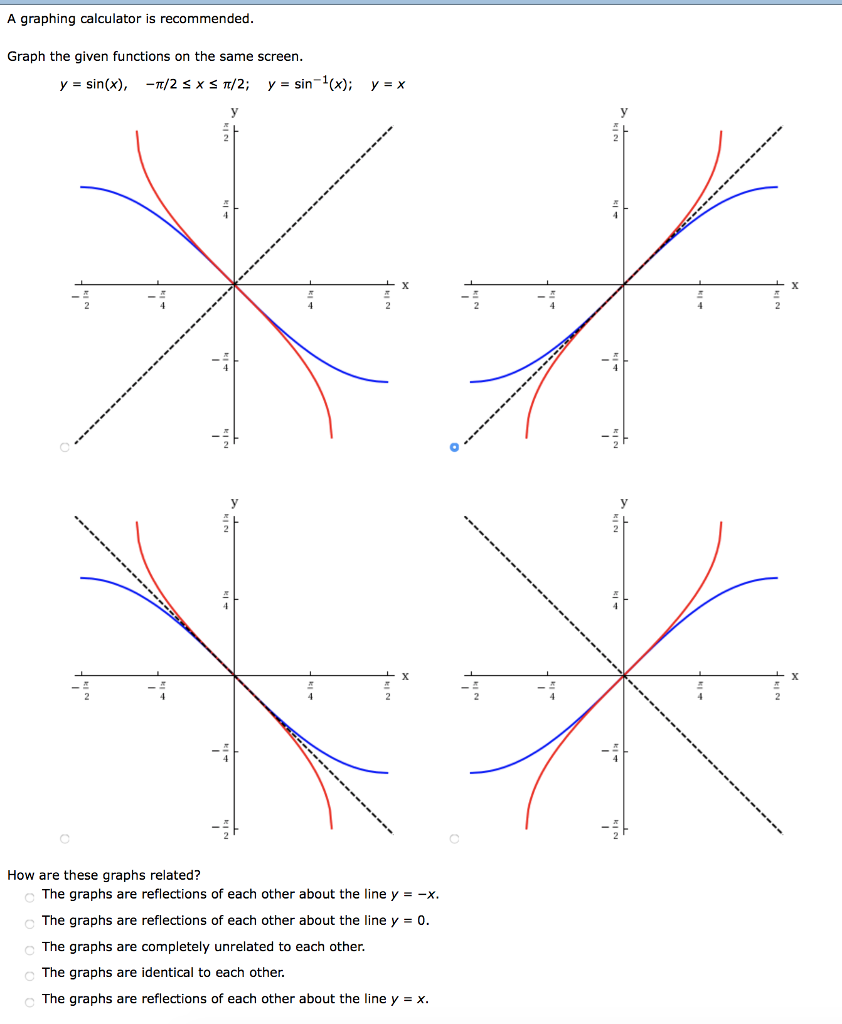
Solved A Graphing Calculator Is Recommended Graph The Gi Chegg Com

Answered Suppose P 2 1 Is A Point On A Bartleby

12/21/ · 43 Derivatives and the Shape of a Graph 194) If c is a critical point of \(f(x)\), when is there no local maximum or minimum at \(c\)?Show the transformation of the graph of \(y=\sin x\) into the graph of \(y=2 \sin(4x−\frac{π}{2})2\) Solution Consider the series of graphs in Figure \(\PageIndex{1}\) and the way each change to the equation changes the image Figure \(\PageIndex{2}\) The basic graph8/3/13 · It's not sin(x) That function has no vertical asymptotes, hence answers A and C are eliminated The answer is option D II and IV only Sorry I don't have any great 'explanation' for that

Trig Graphs And Equations Ppt Download

7 3 Polar Coordinates Calculus Volume 2 Openstax

π 2 π −π 0 −π 2 x y This time, the graph illustrates that tan(θ π) ≡ tanθ which implies that tanθ is a periodic function with primitive period π We may also observe that tan(−θ) ≡ −tanθ which makes tanθ an "odd function" 322 GRAPHS OF MORE GENERAL TRIGONOMETRIC FUNCTIONSThe formula for the period of a pendulum is T = 2π * √(L/g) where T is the period in seconds and L is the length in meters By squaring both sides of the equation the formula becomes T^2 = (4 * pi^2 * L)/g The relationship of T^2 and L is that ofThe period is 2 π ω = 2 π π = 2 2 π ω = 2 π π = 2 (Recall that we sometimes refer to B B as ω) ω) One cycle of the graph can be drawn over the interval 0, 2 0, 2 To find the key points, we divide the period by 4 Make a table similar to Table 2, starting with x = 0 x = 0 and then adding 1 2 1 2 successively to x x and

What Is This Graphed Function With Asymptotes At P 2 And P 2 Mathematics Stack Exchange

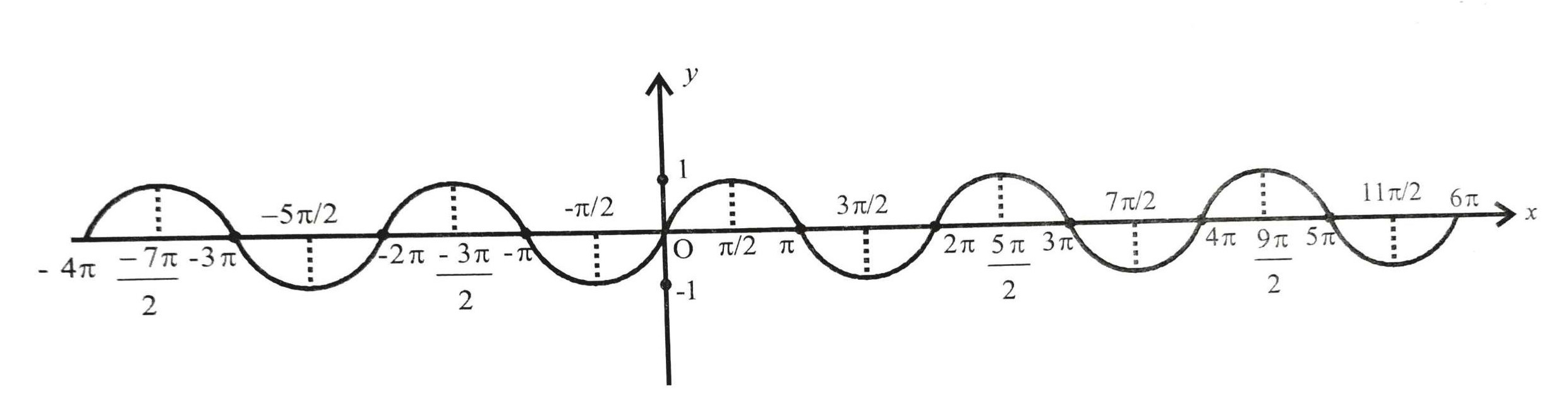
Limits Of Trigonometric Functions Class 11 Maths Geeksforgeeks

12/28/16 · π/2 to π second quadrant, so reference angle = π angle, π to 3π/2 third quadrant, so reference angle = angle π, 3π/2 to 2π fourth quadrant, so reference angle = 2π angle 10π/9 is a bit more than π, so it lies in the third quadrant In this example, the reference angle is reference angle = angle π = π/9Trigonometry (8th Edition) Edit edition Problem 15P from Chapter 47 Graph y = tan x for x between −π/2 and π/2, and then reflect Get solutions4/15/18 · We say the cosine curve is a sine curve which is shifted to the left by `π/2\ (= 157 = 90^@)` The value of the cosine function is positive in the first and fourth quadrants (remember, for this diagram we are measuring the angle from the vertical axis),

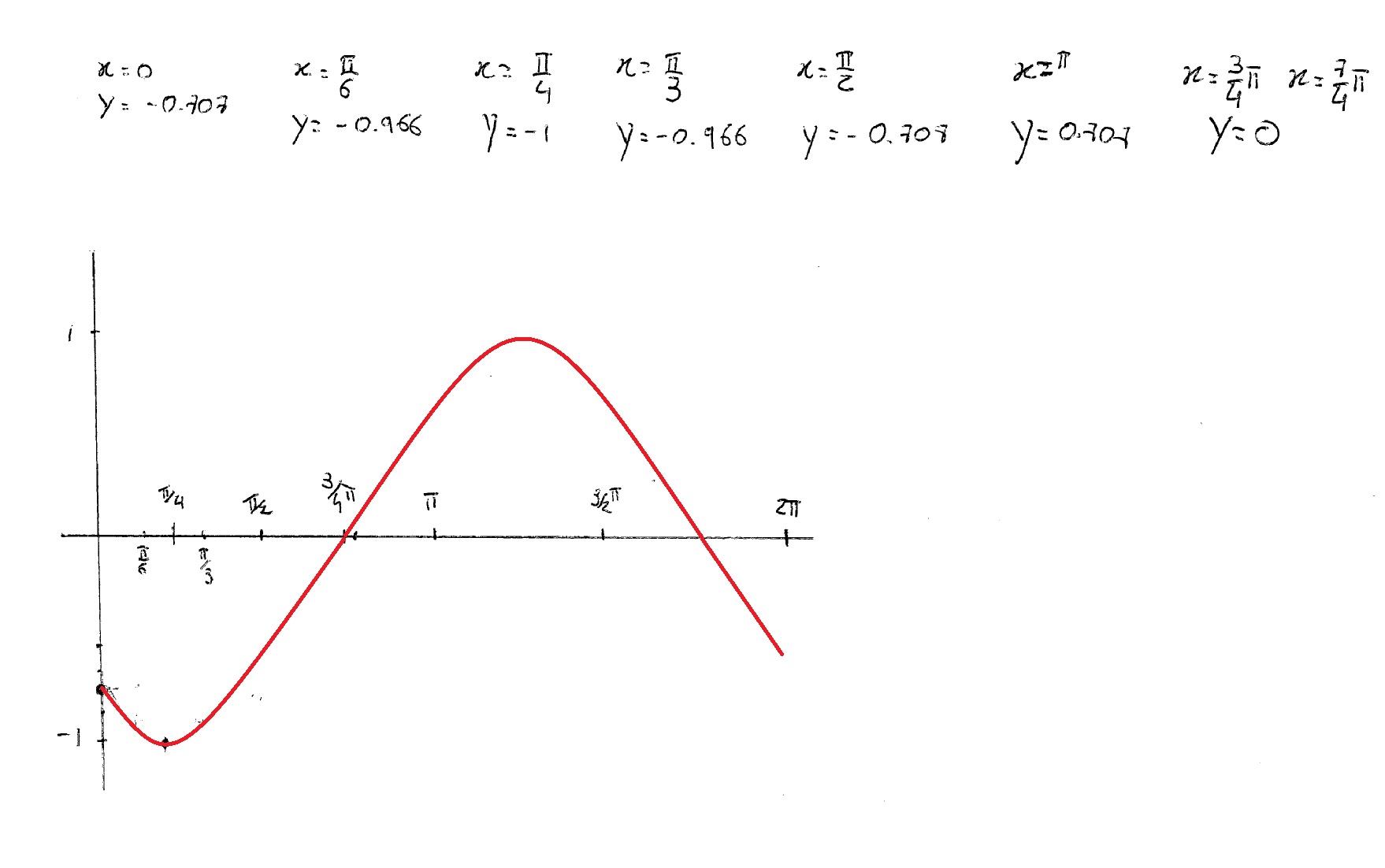
How Do You Graph Y Cos X Pi 4 Socratic

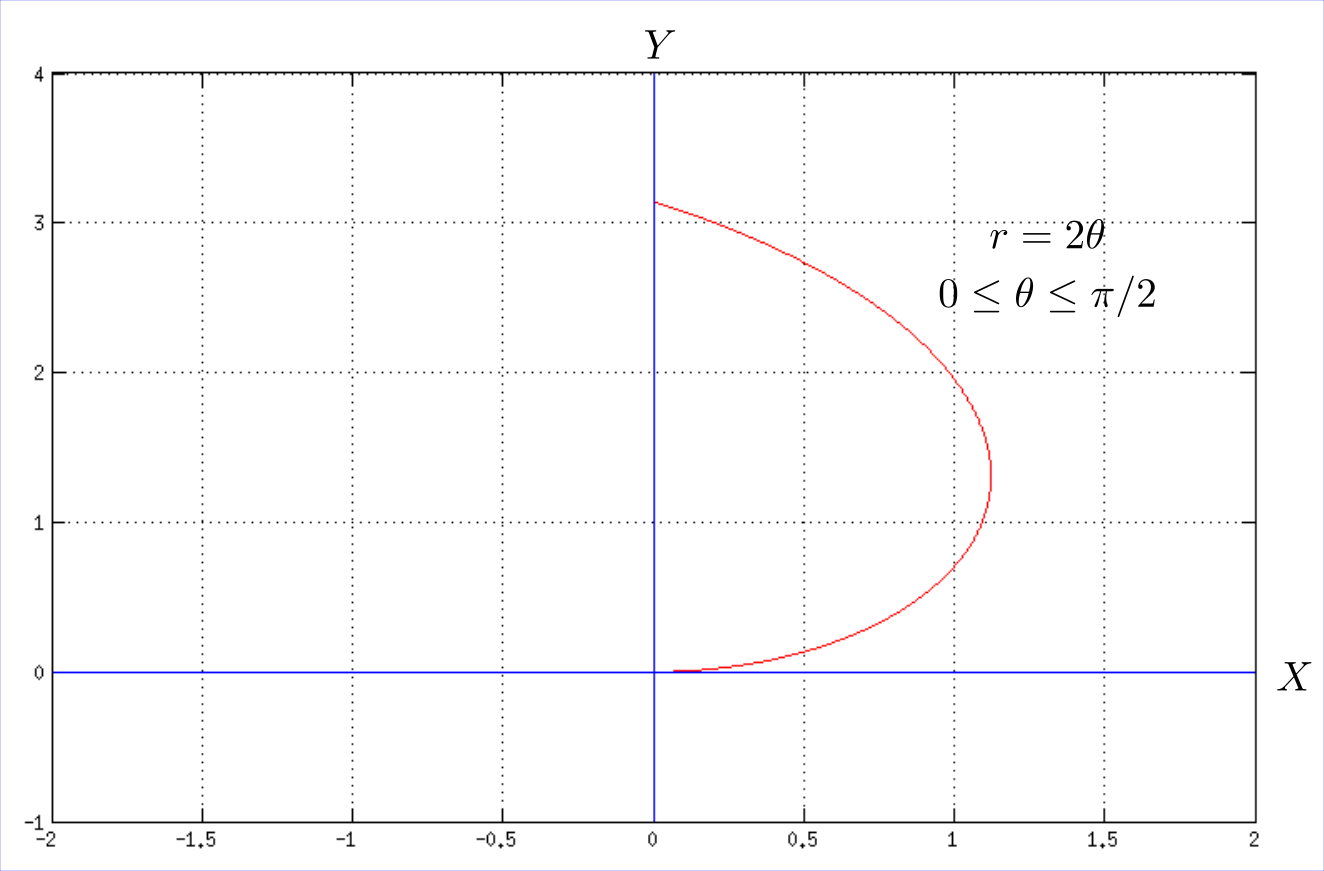
Graph The Polar Equation Over The Given Interval Use The Integration Capabilities Of The Graphing Utility To Approximate The Length Of The Curve Accurate To Two Decimal Places Polar Equation R

Explain 195) For the function \(y=x^3\), is \(x=0\) both an inflection point and a local maximum/minimum?π/2 (radian) = 90 (degree) − π/2 ≤ x ≤ π/2 y = sin 2 x cos 2 x when x = π/2 or 90 degree y = sin 2 (90) cos 2 (90) = 1 when x = 0 y = sin 2 (0) cos 2 (0) = 1 when x = π/2 or 90 degree y = sin 2 (90) cos 2 (90) = 1 Thus, for any value of x between π/2 and π/2, y is always 1 Graph H shows a line that has a constant value y = 1 for any value of x Ans HGraph of the polar function r = 4sinθ 1 area = 35 2 π 2 area = 18π 3 area = 33 2 π correct 4 area = 17π 5 area = 35π Explanation The area of a region bounded by the graph of the polar function r = f(θ) and the rays θ = θ0, θ1 is given by the integral A = 1 2 Z θ 1 θ0 f(θ)2dθ On the other hand, the graph of r = 4 sinθ

What Are Periodic Functions Expii

1 Graph Of The Lagrangian Basis Functions 1 P Np 1 P In Download Scientific Diagram

Here is my graph https//wwwdesmoscom/calculator/l8o2bapufk If you do not want to visit the link, here is a screenshot The dashed line is the builtin sin(x) function The superimposed orange line is an approximation function My question is Why is desmos only plotting the part between π/2 and π/2 ?Graph of the tangent function from = π/2 When calculations are performed manually, the necessary quadrant corrections and exception handling can be done by inspection, but it is more useful to have a single function that always gives an unambiguous correct resultHow do you graph #y = 3 sec(2x)#?

Graphs Of Trigonometric Functions Sine Cosine Tangent Etc

Graph Y 2sin 2x P 1 Youtube

Arcsin definition The arcsine of x is defined as the inverse sine function of x when 1≤x≤1 When the sine of y is equal to x sin y = x Then the arcsine of x is equal to the inverse sine function of x, which is equal to y arcsin x = sin1 x = y Example arcsin 1 = sin1 1Outward to the point (1,π 2, 2) in rectangular coordinates), then 4 returns to the origin as θ moves to point "up" Figure 1 Graph of r = sin 2θ for 0 < θThe result of the transformation is to shift the graph vertically by − 22 − 2 in the y y ydirection and stretch the graph vertically by a factor of 5 5 5 Since the graph is not stretched horizontally, the period of the resulting graph is the same as the period of the function sin ⁡ (x) \sin(x) sin (x), or 2 π 2\pi 2 π _\square

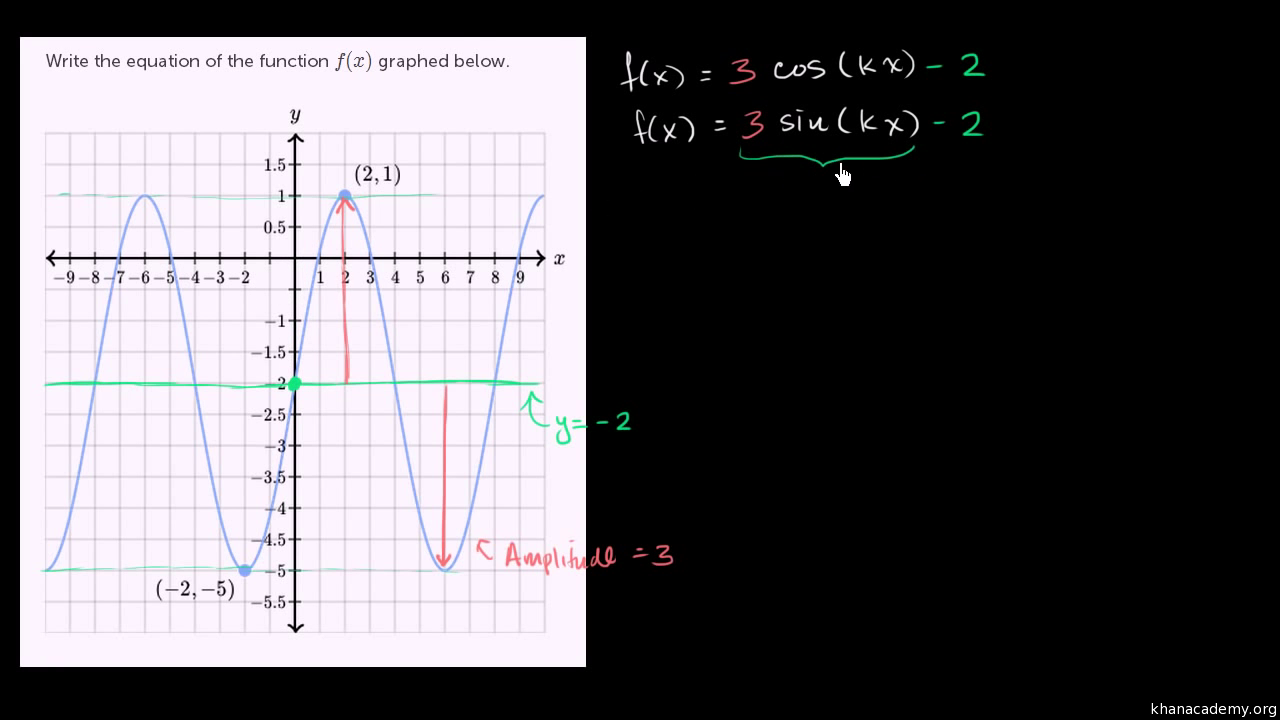
Sinusoidal Function From Graph Video Khan Academy

Draw The Graph Of F X Tan X Cot X

A r Q y x Figure 1 Off center circle r = 2a cos θ √ π 3π, cosθ= − 2 √ 2 in the direction of angle When < θπ, risPrecalculus Graph y=2sin (xpi/2) y = 2sin(x − π 2) y = 2 sin ( x π 2) Use the form asin(bx−c) d a sin ( b x c) d to find the variables used to find the amplitude, period, phase shift, and vertical shift a = 2 a = 2 b = 1 b = 1 c = π 2 c = π 2 d = 0 d = 0 Find the amplitude a aTextbook solution for Precalculus Mathematics for Calculus 6th Edition 6th Edition Stewart Chapter 54 Problem 41E We have stepbystep solutions for

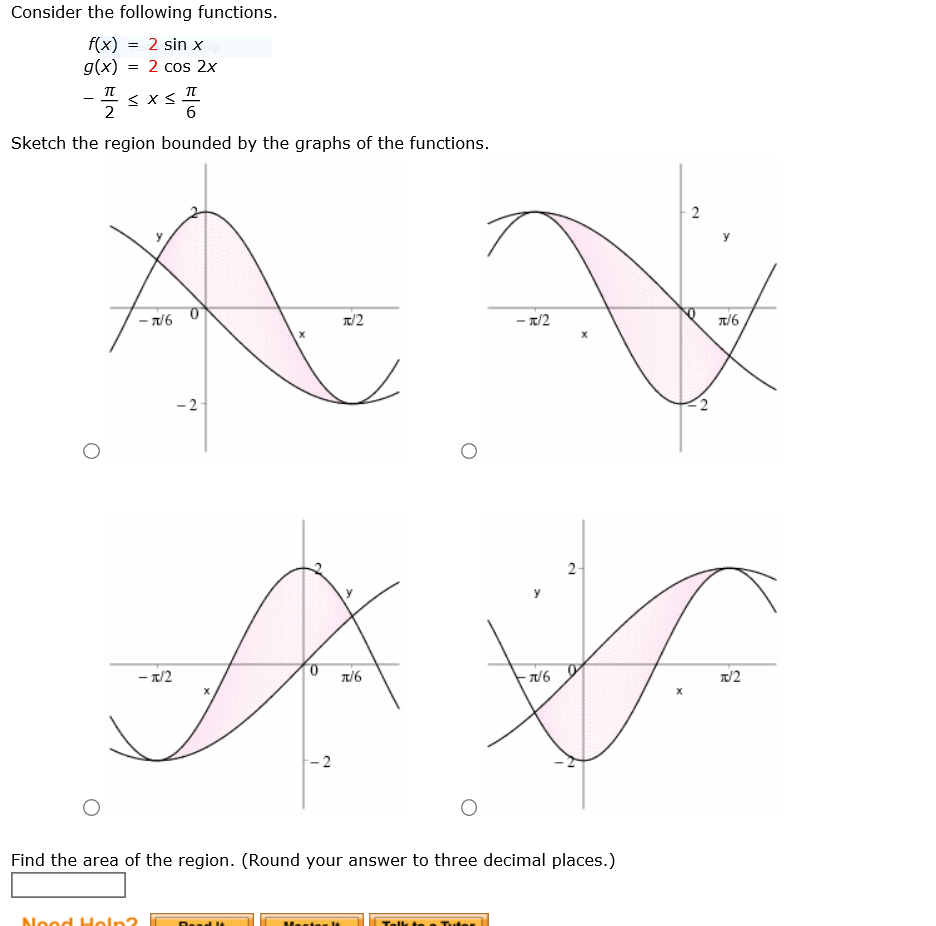
Solved Consider The Following Functions F X 2 Sin X G Chegg Com

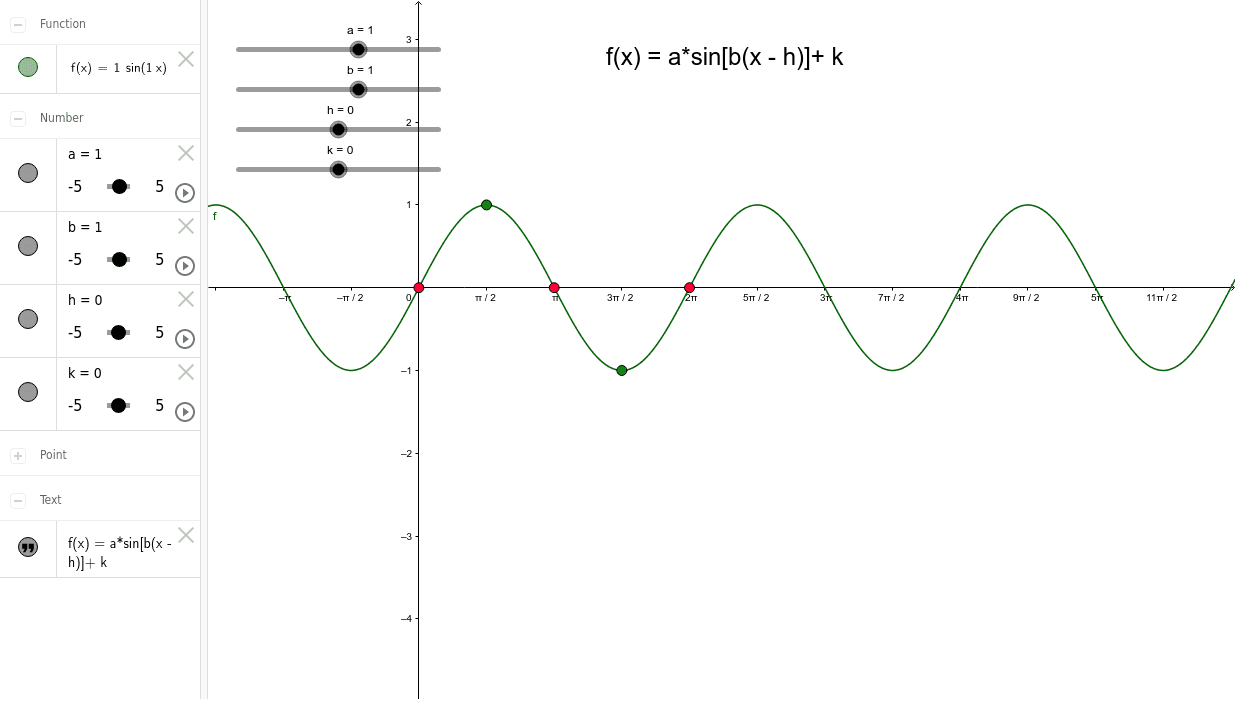
Sine Graph Transformations Geogebra

To the rotation of 0 corresponds the point (1,0) = (cos(0),sin(0)) to the rotation of π/2 (or 90°) corresponds the point (0,1) = (cos(π/2),sin(π/2)) to the rotation of π (or 180°) corresponds the point (1,0) = (cos(π),sin(π)) to the rotation of 3π/2 (or 270°) corresponds the point (0,1) = (cos(3π/2), sin(3π/2)) to the rotation of 2 π (or 360°) corresponds the point (1,0) =The period of the tangent function is π because the graph repeats itself on intervals of kπ where k is a constant If we graph the tangent function on latex−\frac{\pi}{2}\\/latex to latex\frac{\pi}{2}\\/latex, we can see the behavior of the graph on one complete cycle8/1/17 · How do you graph #y=3tan(x(pi/4))# over the interval #pi, 2pi#?

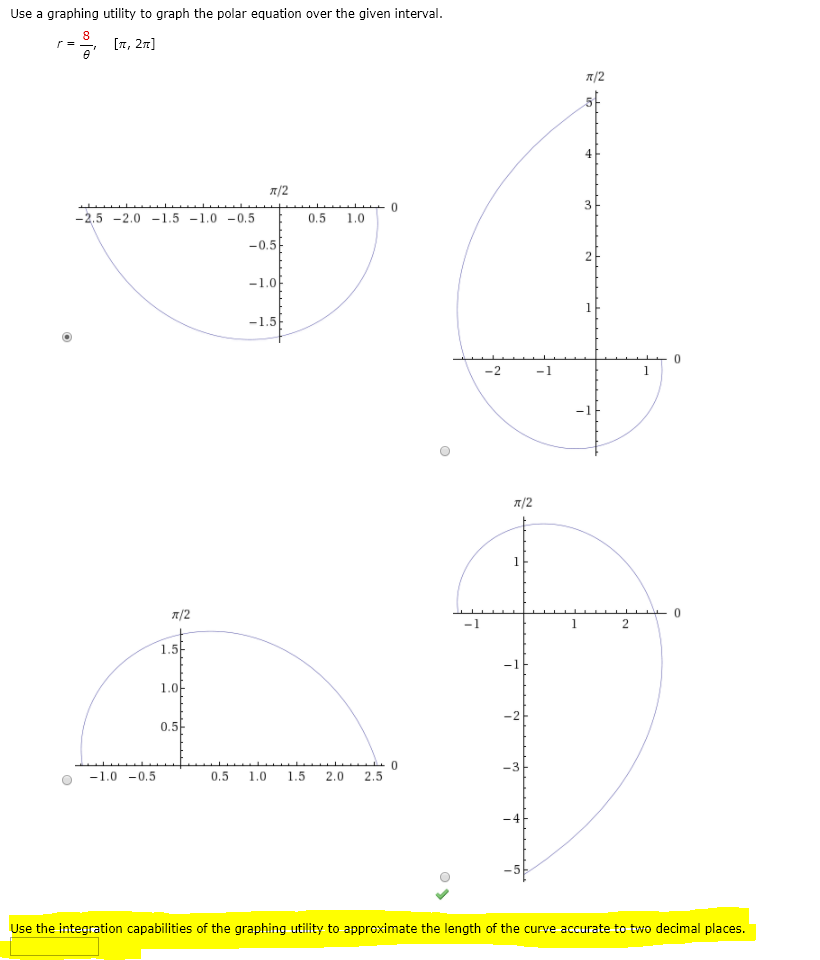
Solved Use A Graphing Utility To Graph The Polar Equation Chegg Com

Graph G T 4sin 3t 2 Use 3 14 For P Use The Sine Tool To Graph The Function The First Point Brainly Com

The graph of y = sin θ, for 0˚ ≤ θ ≤ 360˚ obtained is as shown (π/2) • cos(θ) = cos(θ) Show Stepbystep Solutions Amplitude and Period of Sine and Cosine How to determine the amplitude and period of sine and cosine?

Interpolation Interpolation Is A Process Of Finding A Formula Often A Polynomial Whose Graph Will Pass Through A Given Set Of Points X Y Pdf Free Download

Inverse Of F X Sin X When Restricted To Intervals Other Than Left Frac Pi 2 Frac Pi 2 Right Mathematics Stack Exchange

How To Set Axis Ticks In Multiples Of Pi Python Matplotlib Stack Overflow

Bestmaths

Polar Graphing Supposed Range Is Between 0 To Pi But Graph Drawn Range From Pi 2 To Pi 2 Mathematics Stack Exchange

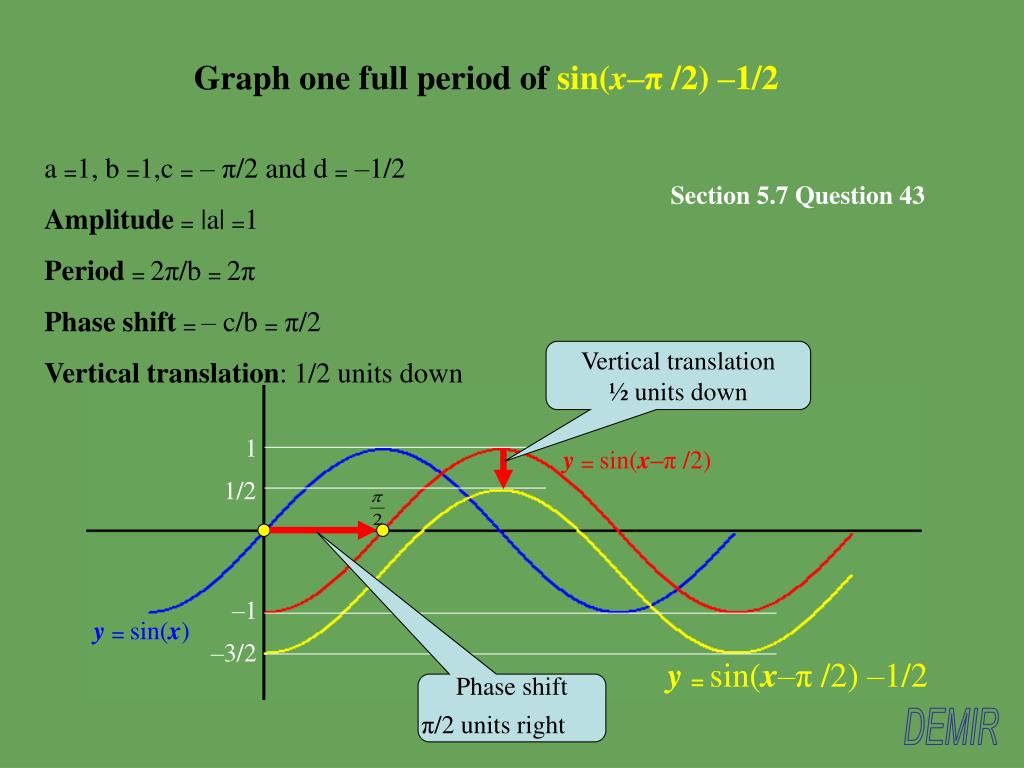
Ppt X Intercepts Powerpoint Presentation Free Download Id

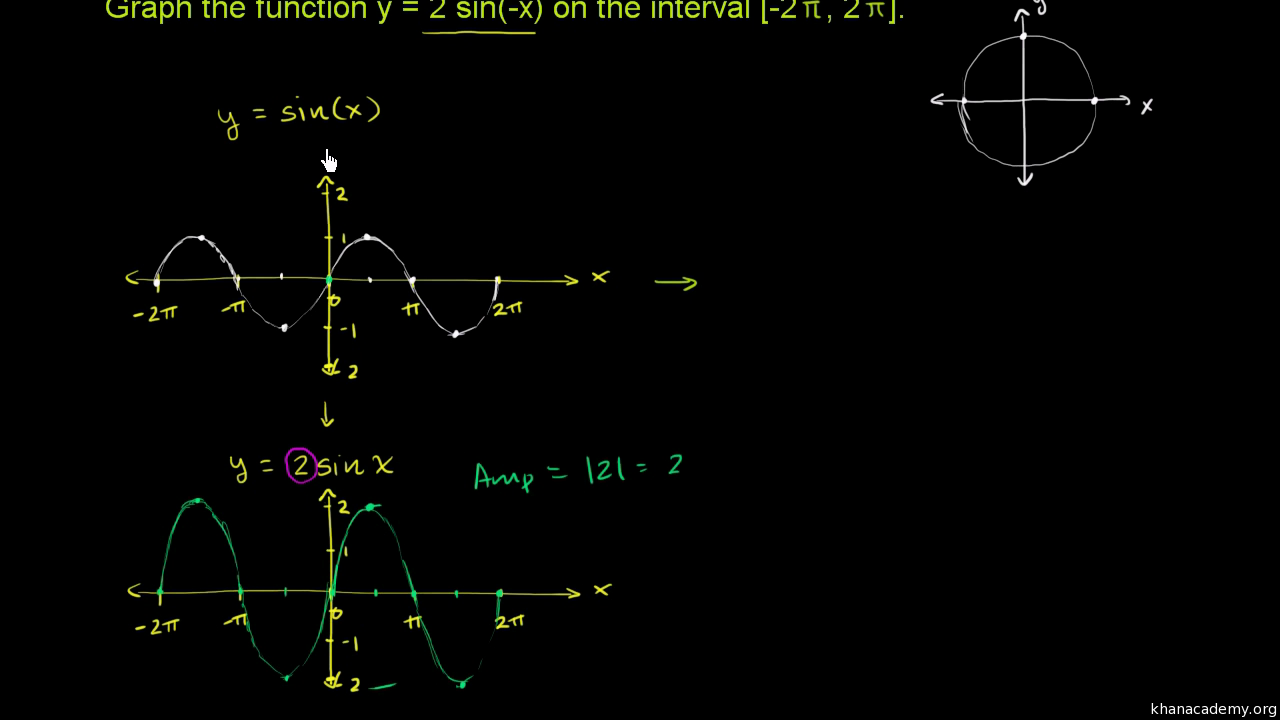
Transforming Sinusoidal Graphs Vertical Stretch Horizontal Reflection Video Khan Academy

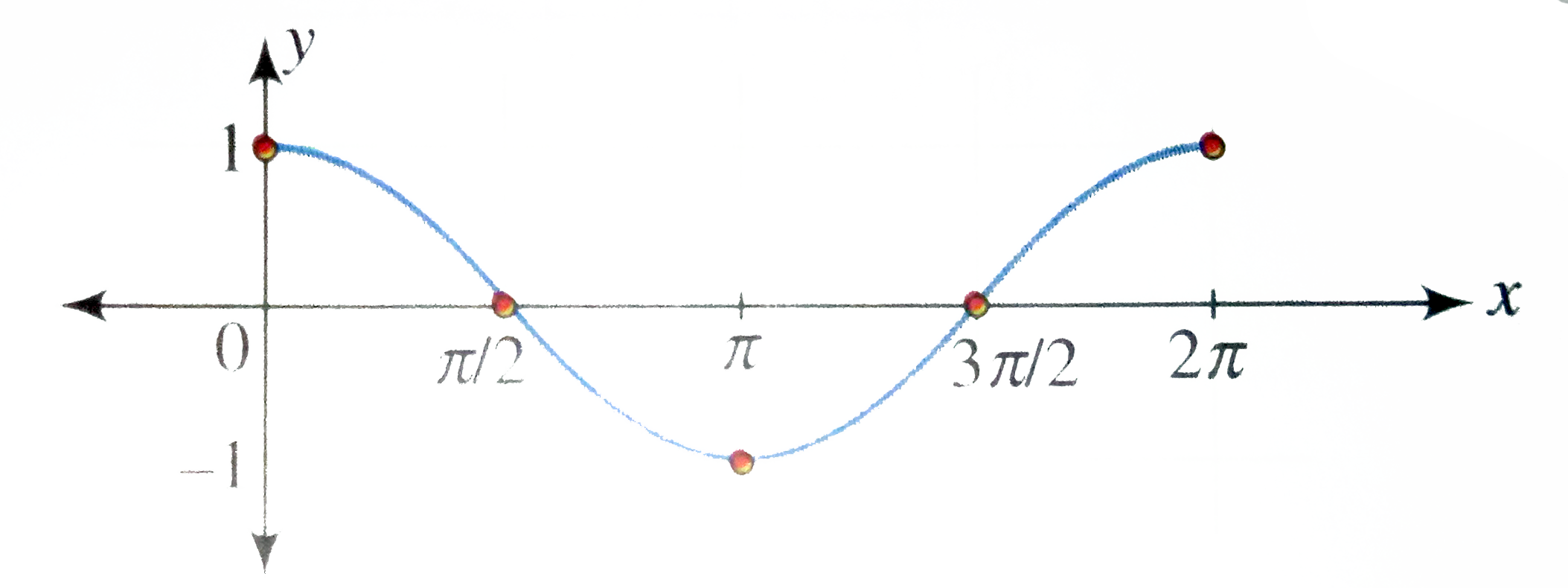
Draw The Graph Of Y Cos X X In 0 2pi Where Repres

Answered Consider The Following X 3 Sec 8 Bartleby

Mfg Polar Coordinates

Find An Expression For The Area Under The Graph Of F As A Limit F X 5x Cos 5x 0 X P 2 Youtube

Cochranmath Sine And Cosine Graphs

Compare The Following Functions F X 2 Sin 2x P 2 G X Graph Of A Quadratic With Points At Brainly Com

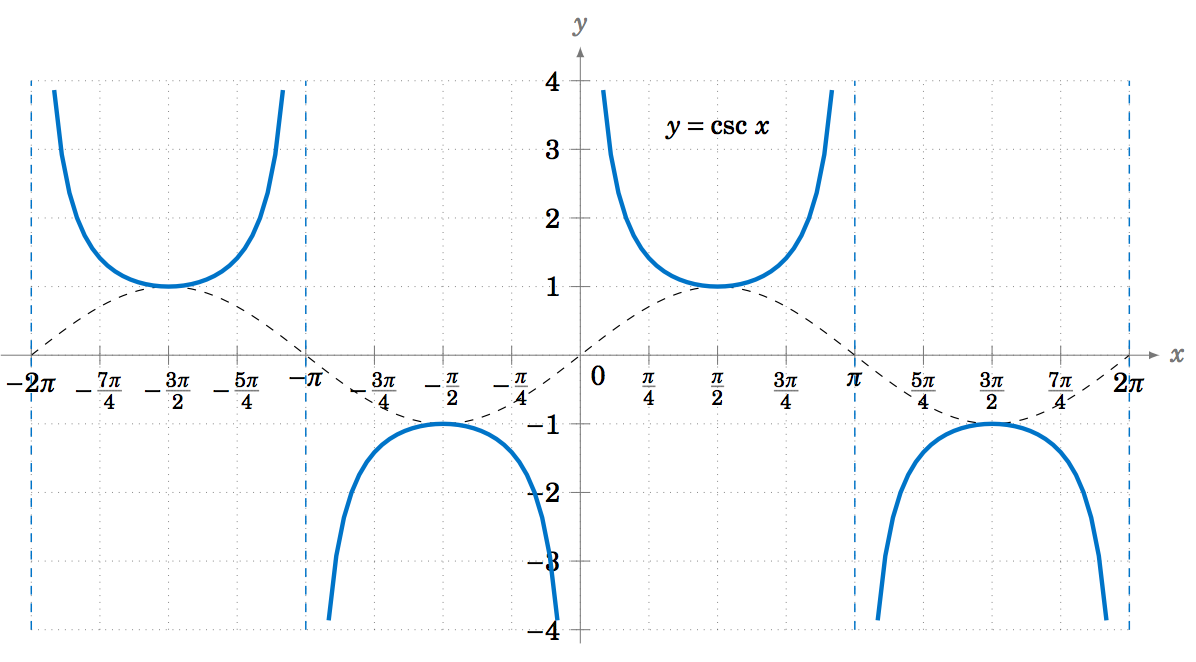
5 1 Graphing The Trigonometric Functions Mathematics Libretexts

Drill For Exam Graph Cie

Graph Y Csc Pi X Math Help Forum

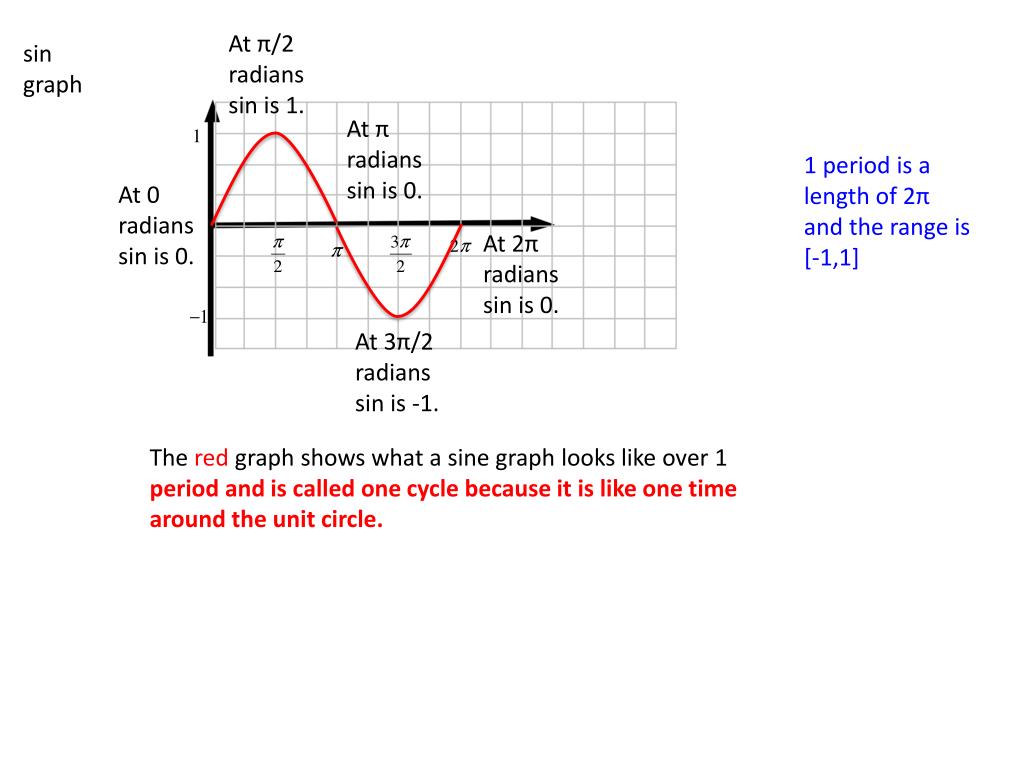
Ppt Sin Graph Powerpoint Presentation Free Download Id

Griffiths Qm

Transformation Of Cos X To Sin X Via Cos X Frac Pi 2 Sin X Mathematics Stack Exchange

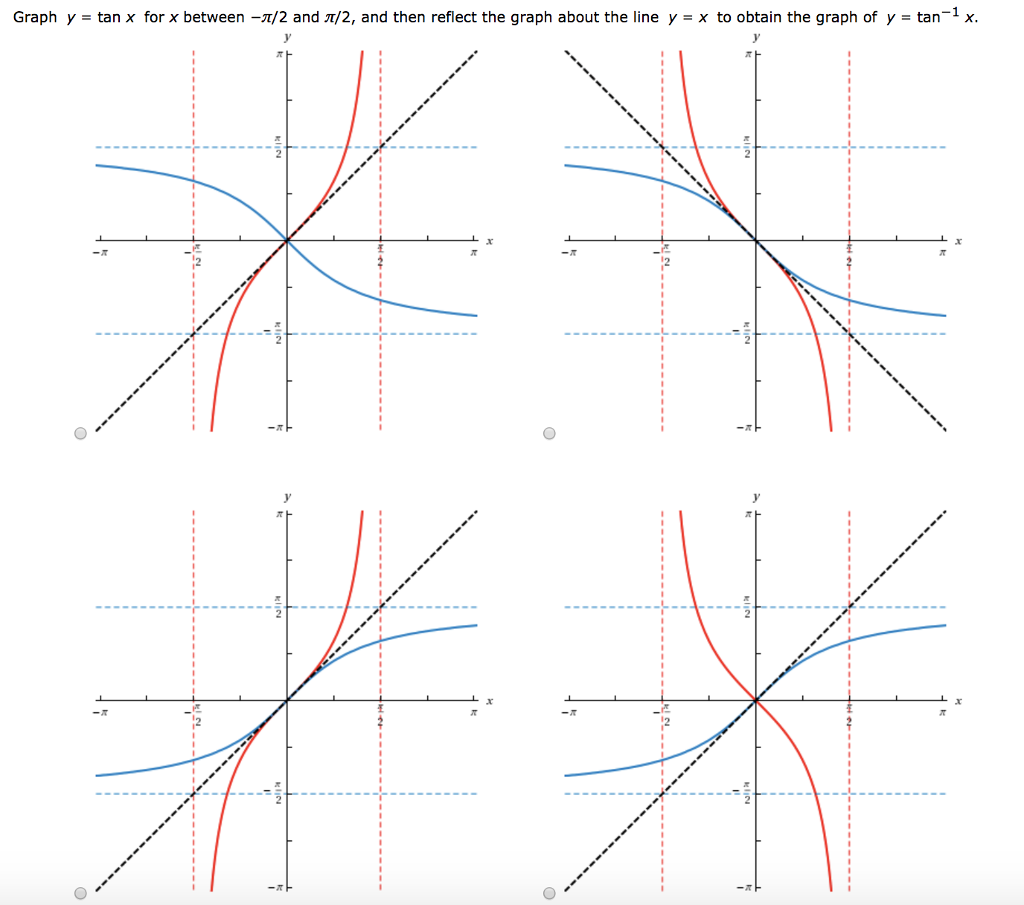
Solved Graph Y Tan X For X Between P 2 And P 2 And Then Chegg Com

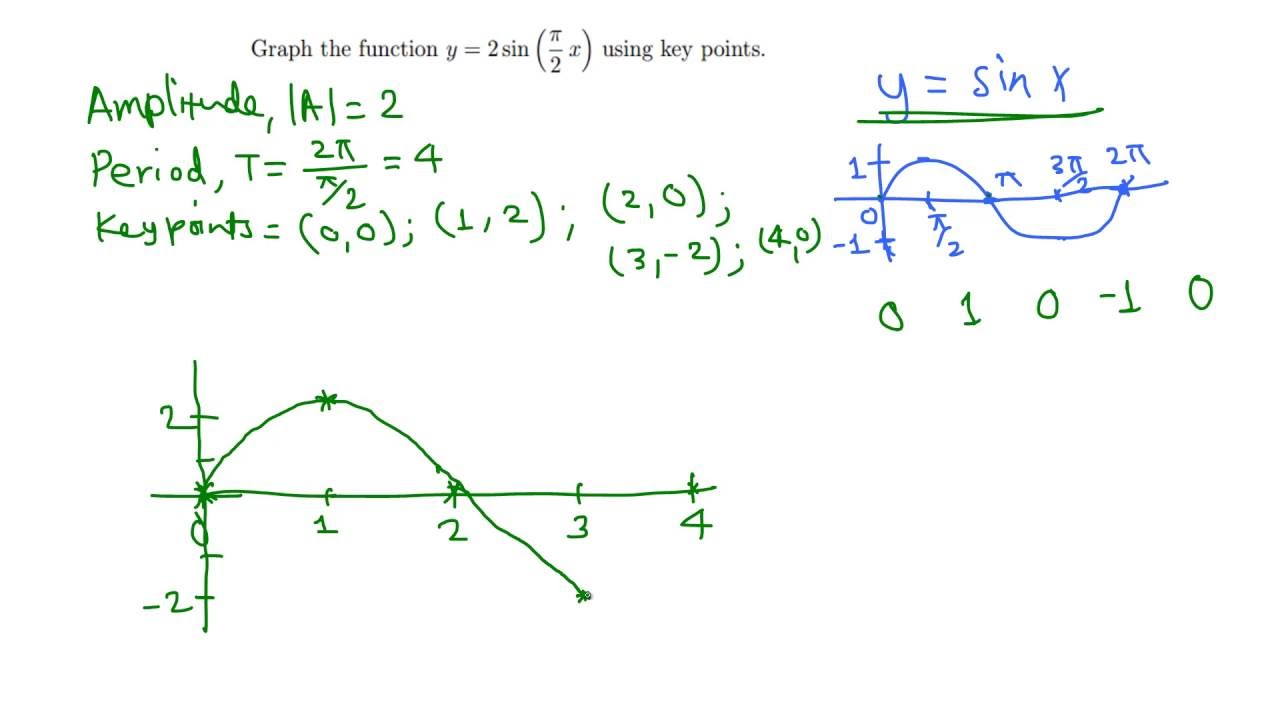
Graph Of Y 2 Sin Pi 2 X Using Key Points Youtube

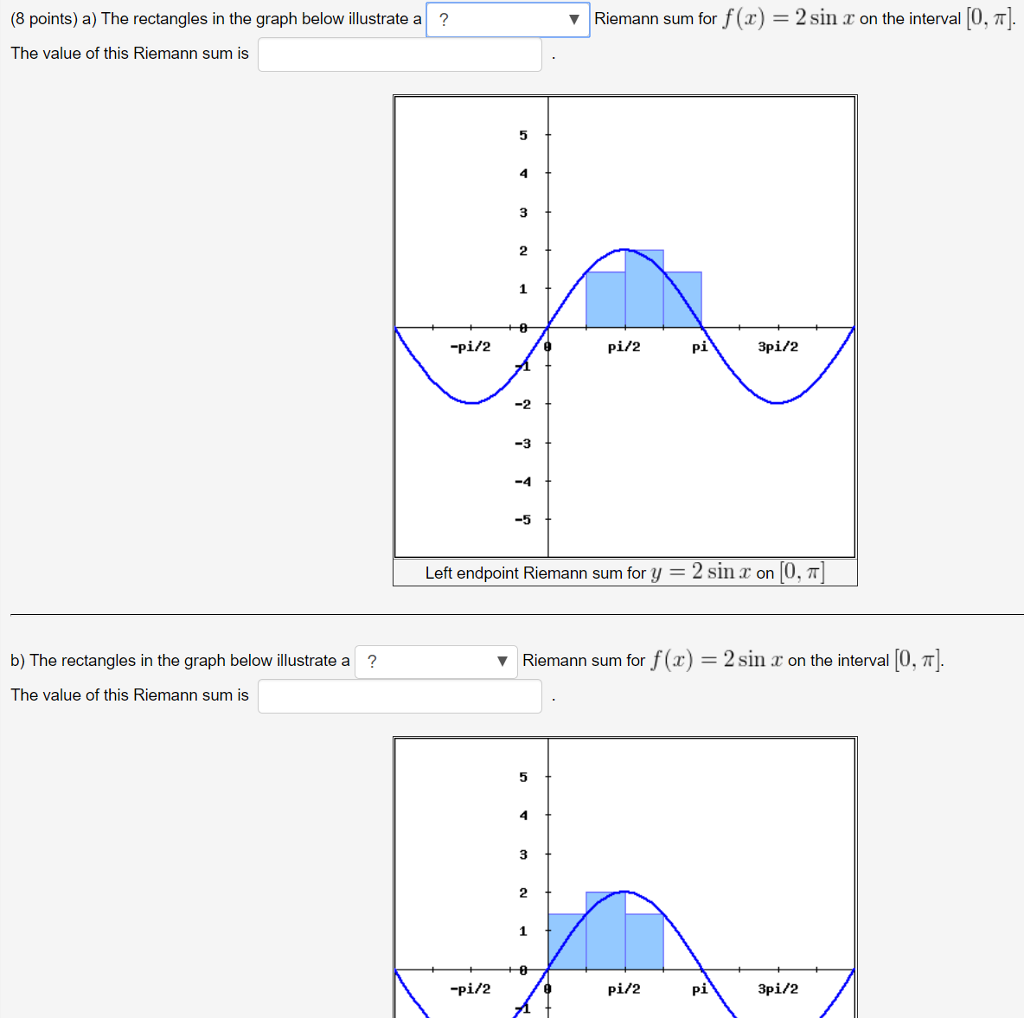
Solved Riemann Sum For F Z 2 Sin R On The Interva Chegg Com

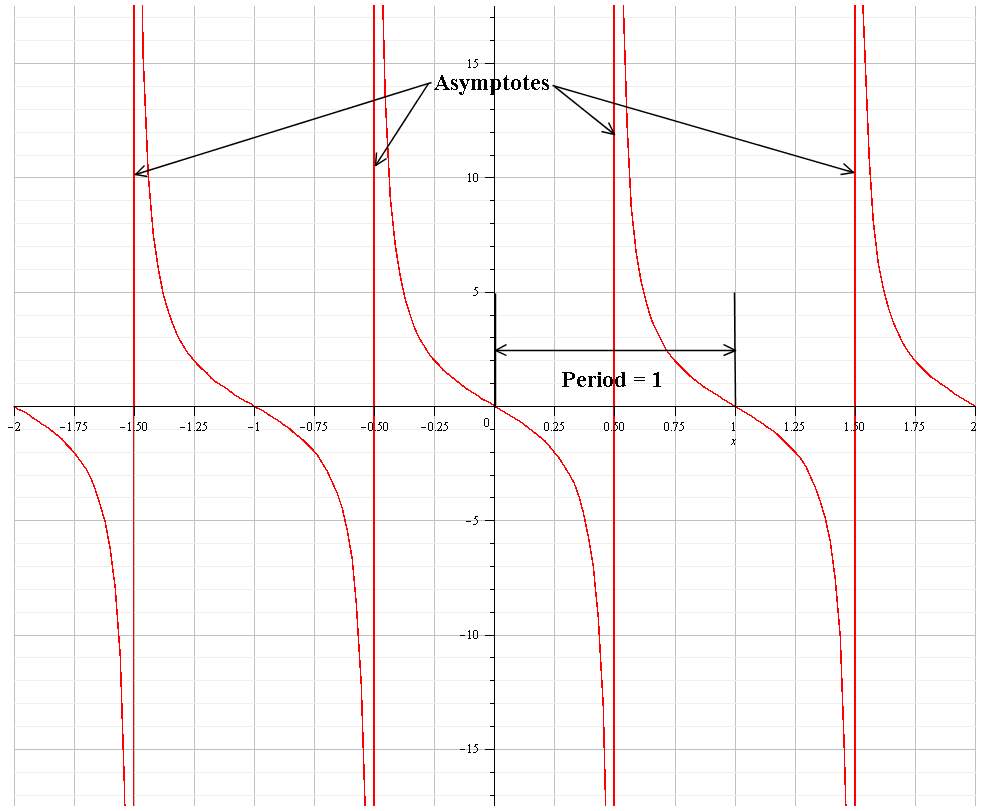
How Do You Identify The Period And Asympotes For Y 2tan Pitheta Socratic

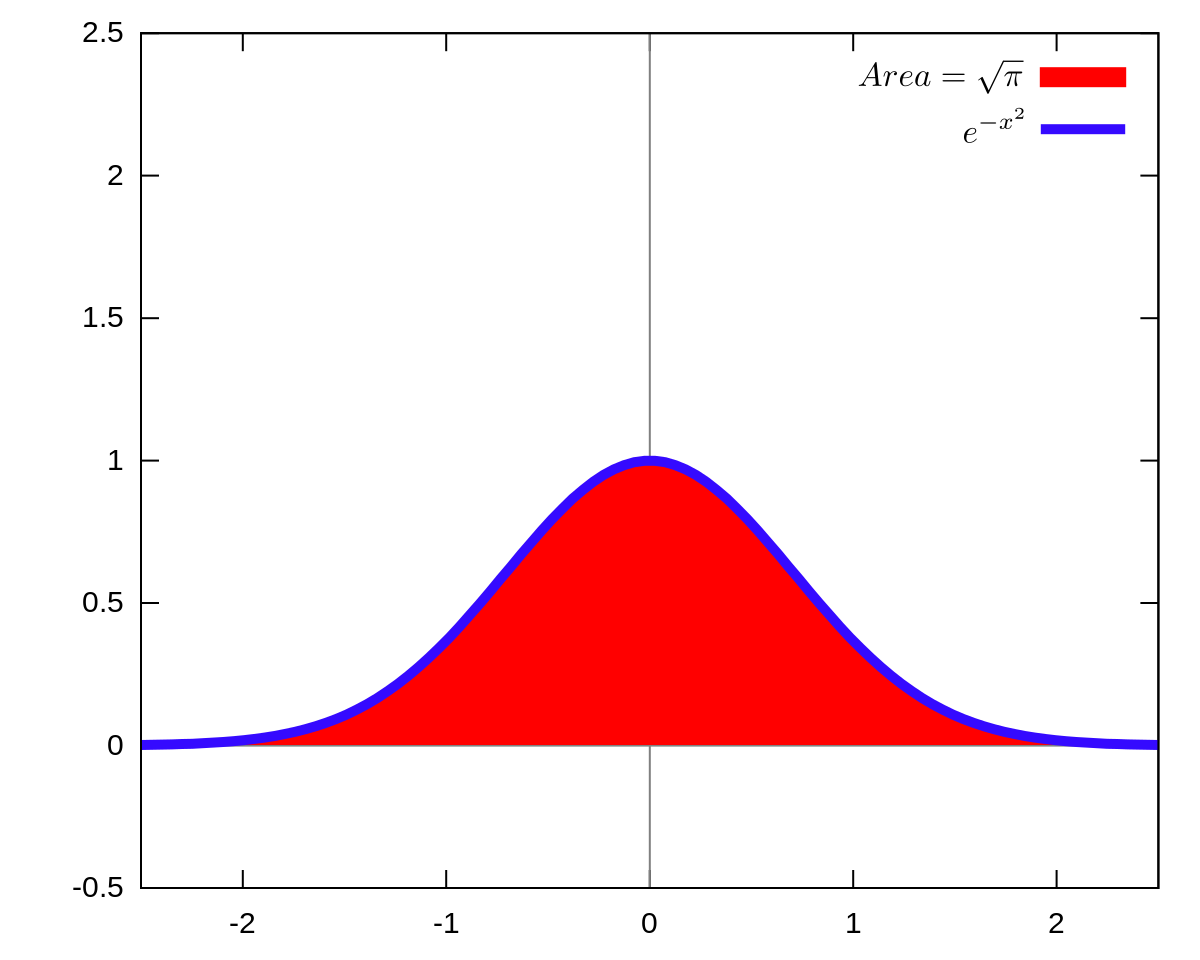
Gaussian Integral Wikipedia

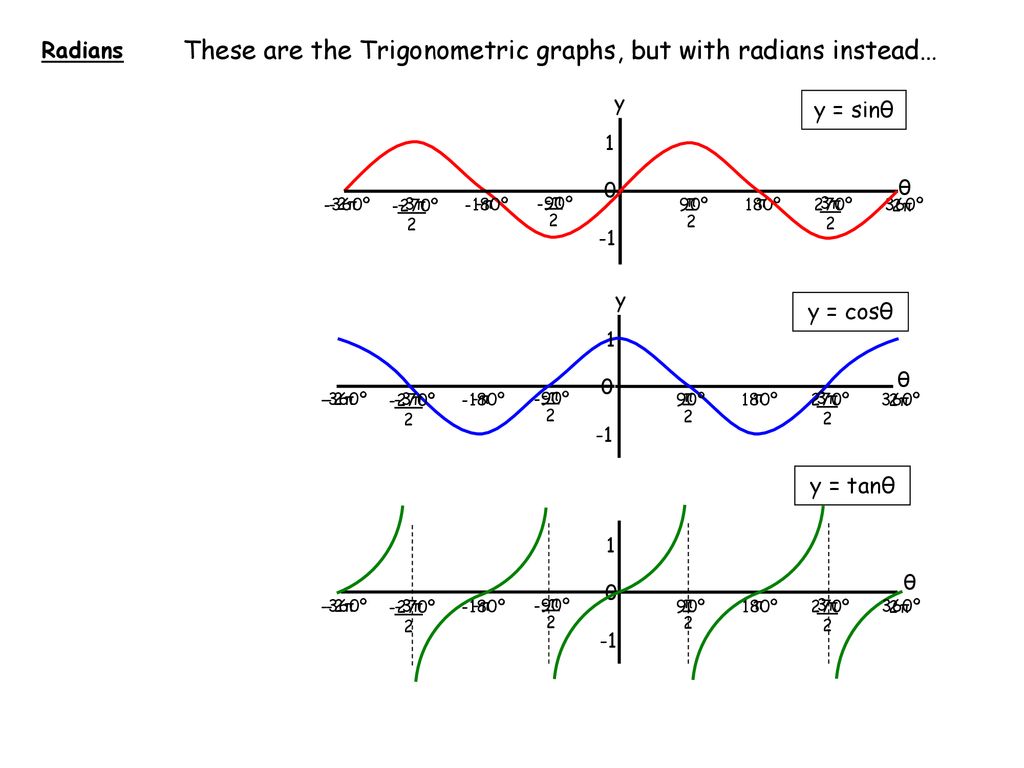
Trig Graphs And Equations Ppt Download

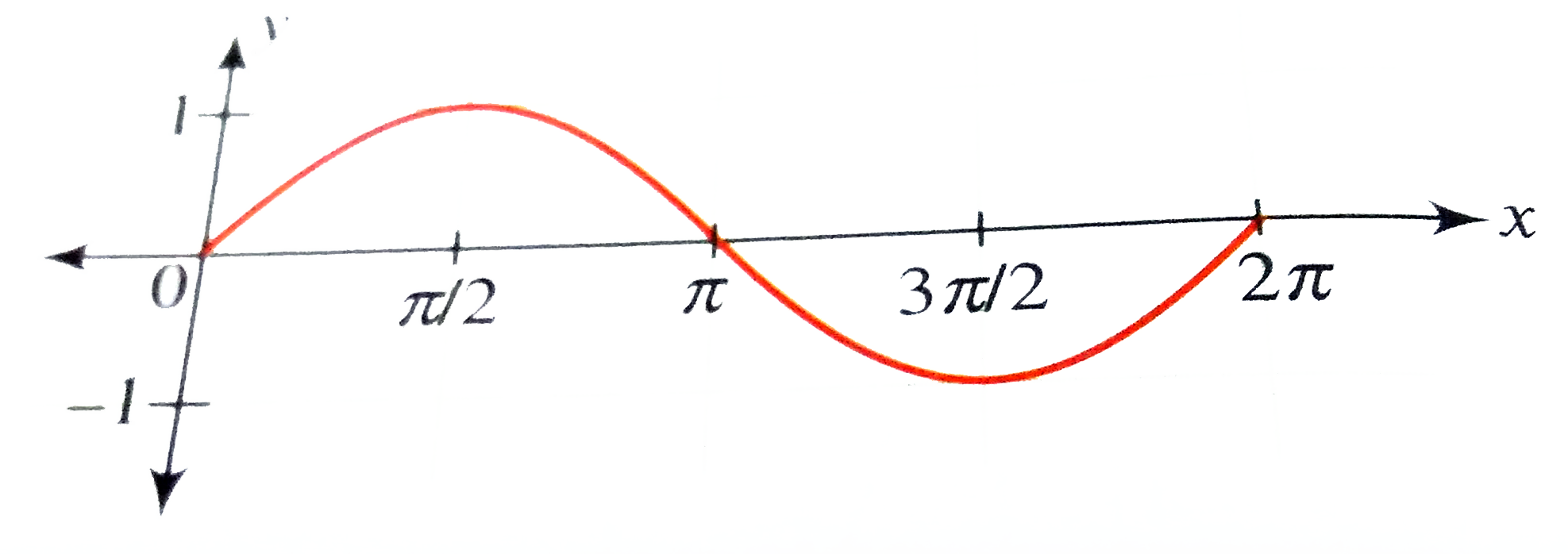
Draw The Graph Of Y Sin X X In 0 2pi Where Repre

Plos Computational Biology Competing Evolutionary Paths In Growing Populations With Applications To Multidrug Resistance

Trig Graphs And Equations Ppt Download

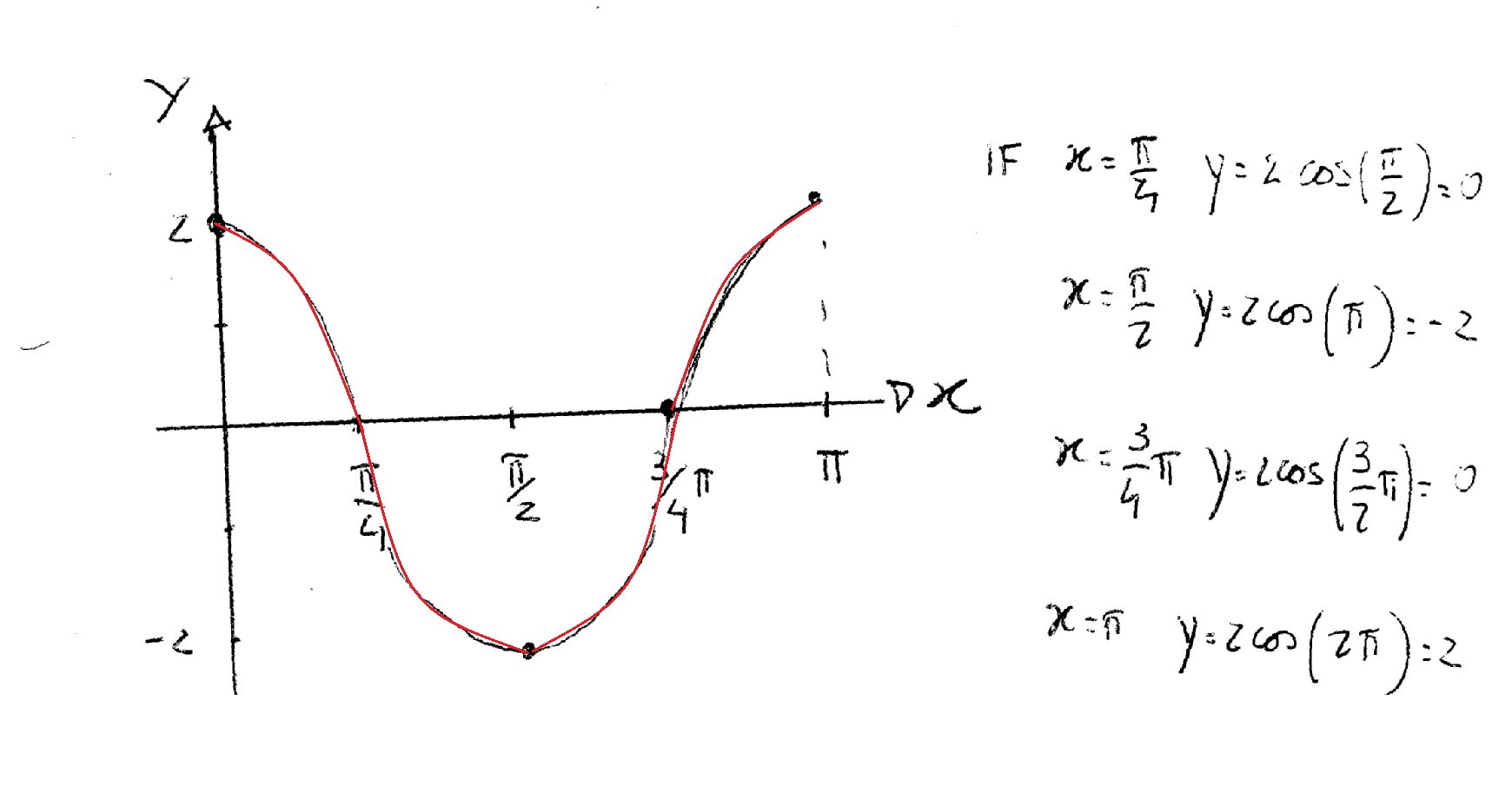
How Do You Graph Y 2cos2x Socratic

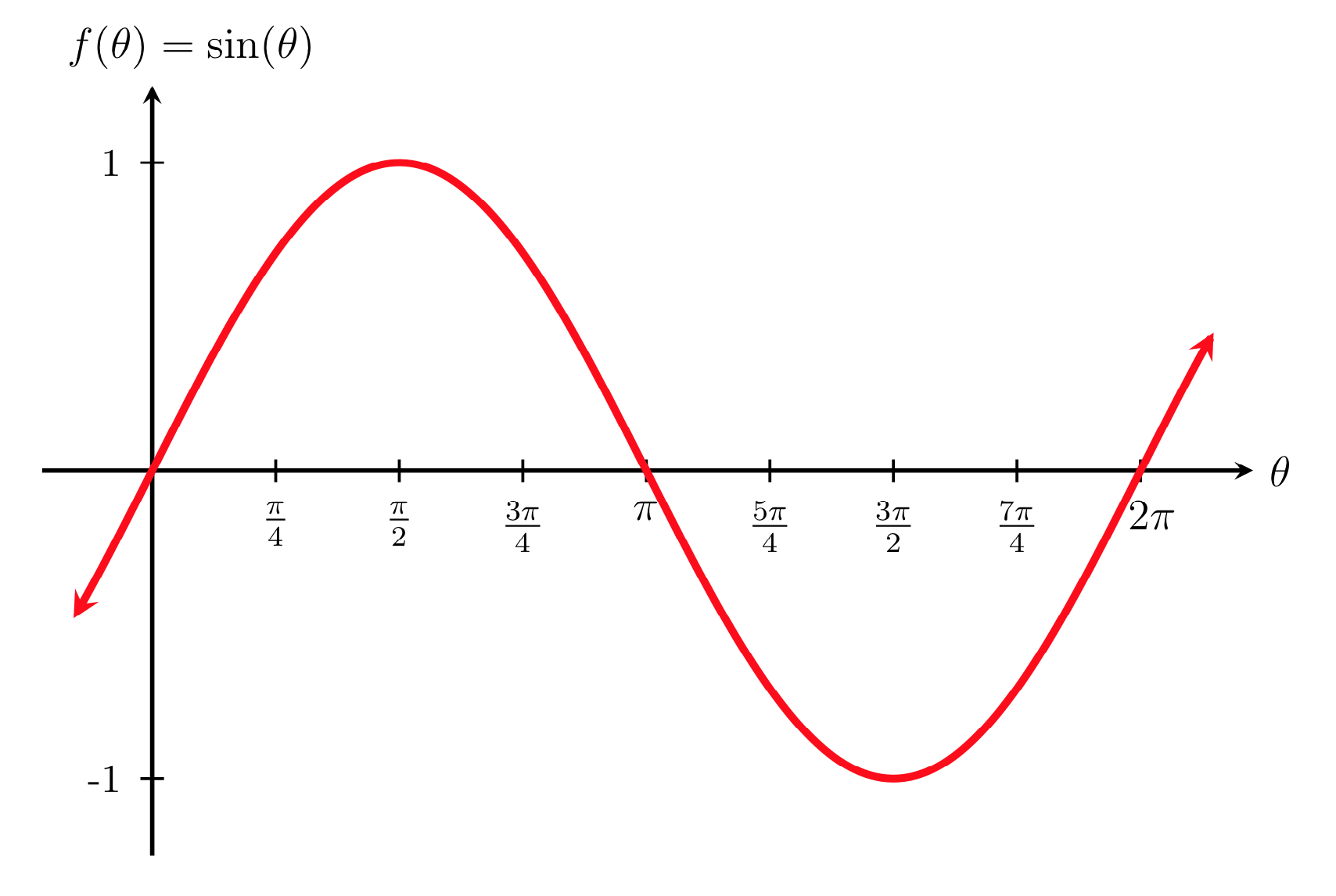
Mfg The Sine And Cosine Functions

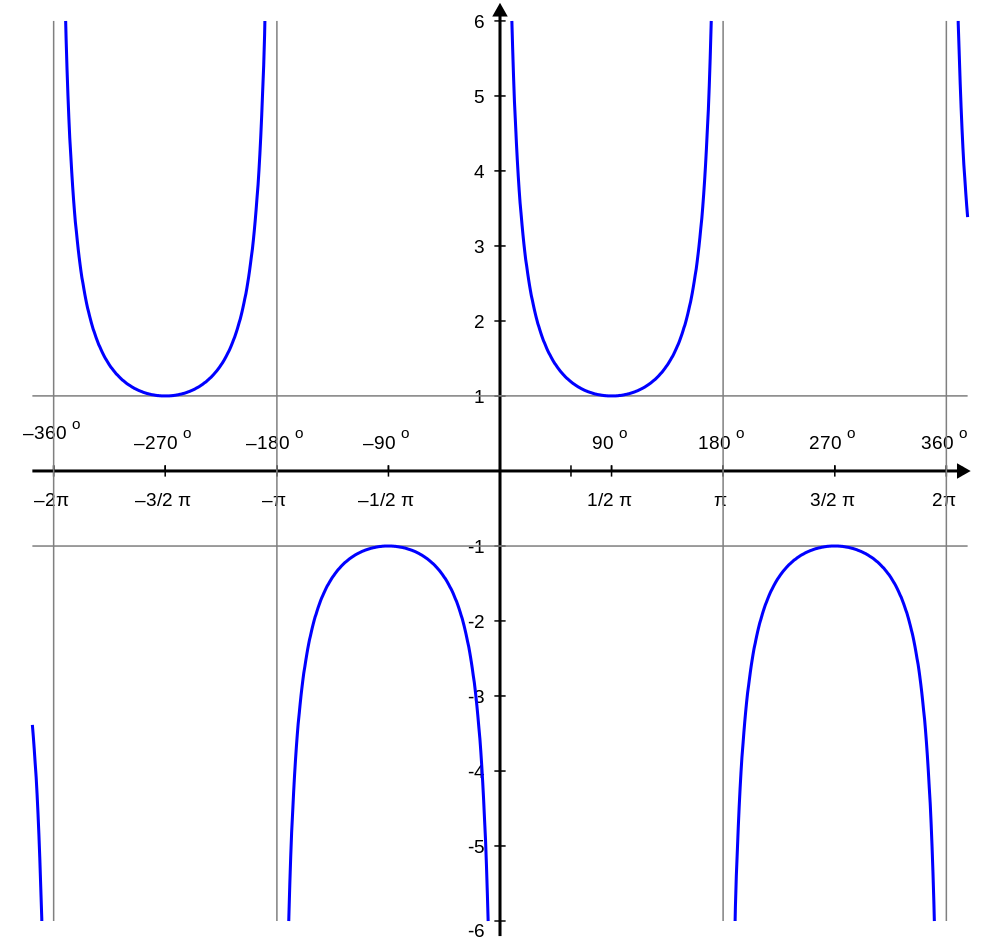
Cosecant And Secant Graphs Brilliant Math Science Wiki

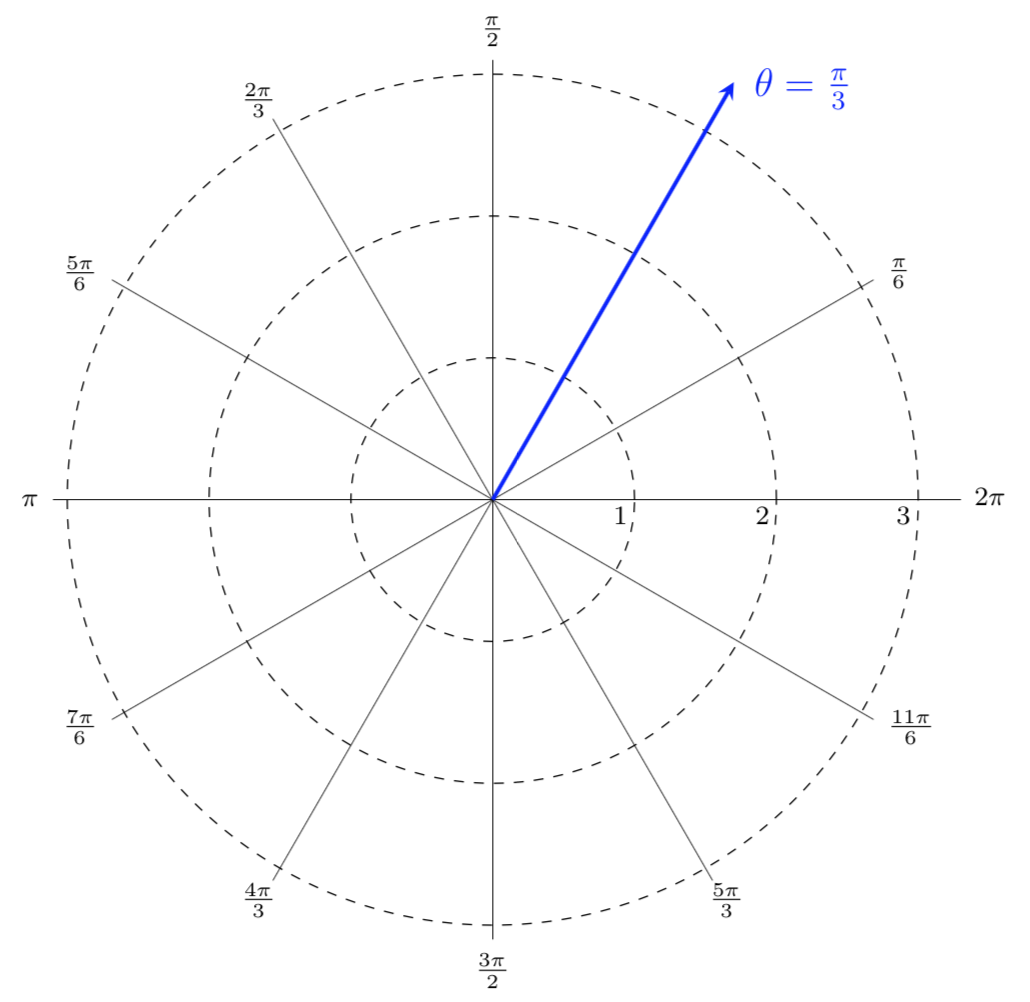
Mfg Polar Coordinates

How To Sketch Polar Curves Krista King Math Online Math Tutor

Qn9yfzh Yttpwm

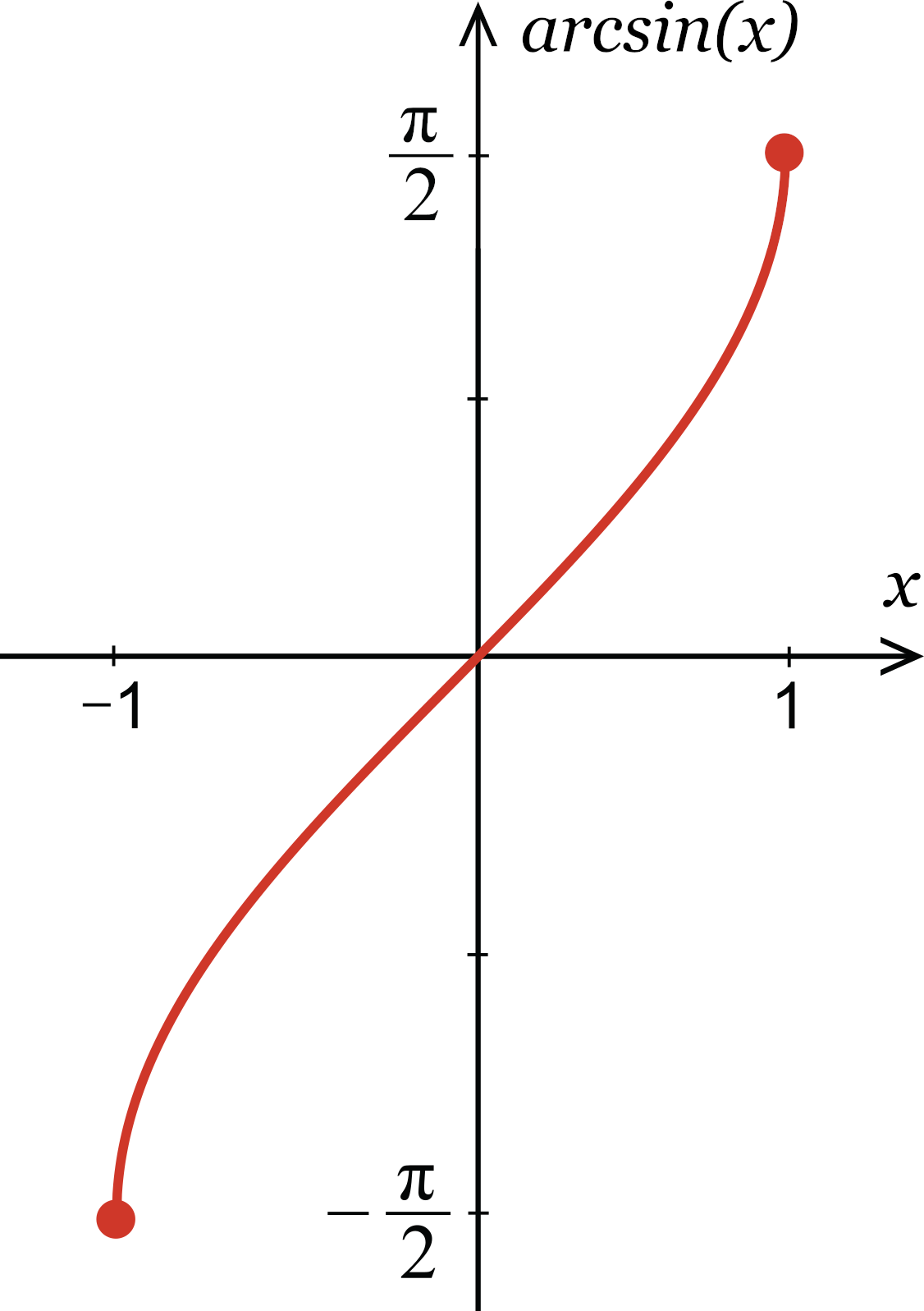
Inverse Sine Calculator Calculate Arcsin X Inch Calculator

Trig Functions Amp Freq Phase Shifts Algebra 2 Trig Mathsux 2

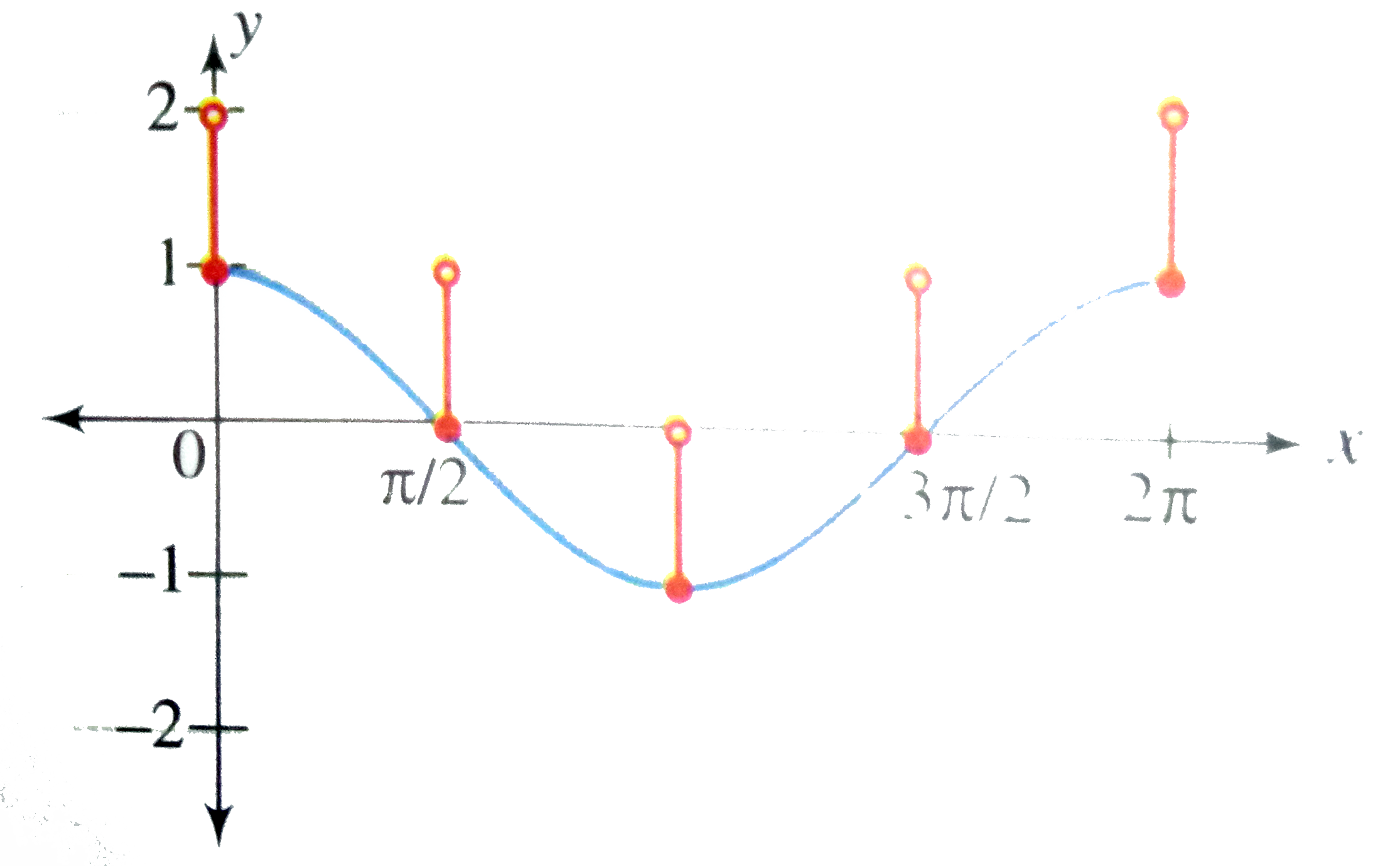
Draw The Graph Of Y Cos X X In 0 2pi Where Denot

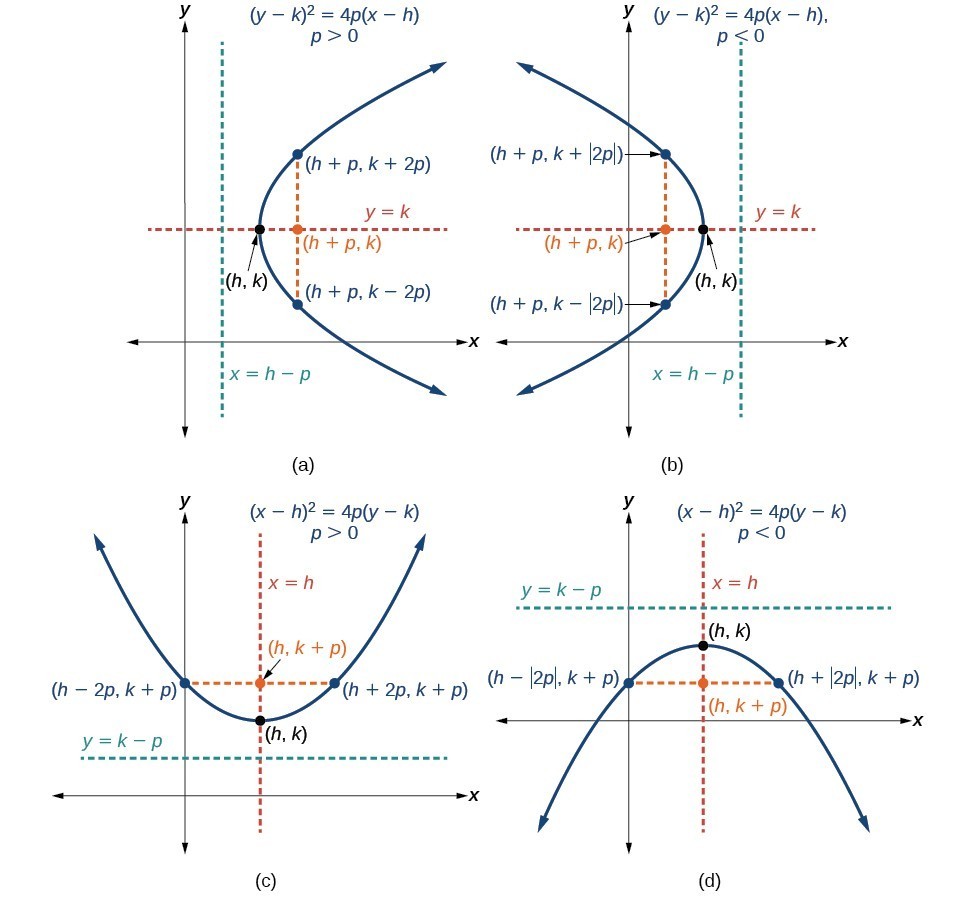
Parabolas With Vertices Not At The Origin College Algebra

Graphs Of Trigonometric Functions Sine Cosine Tangent Etc

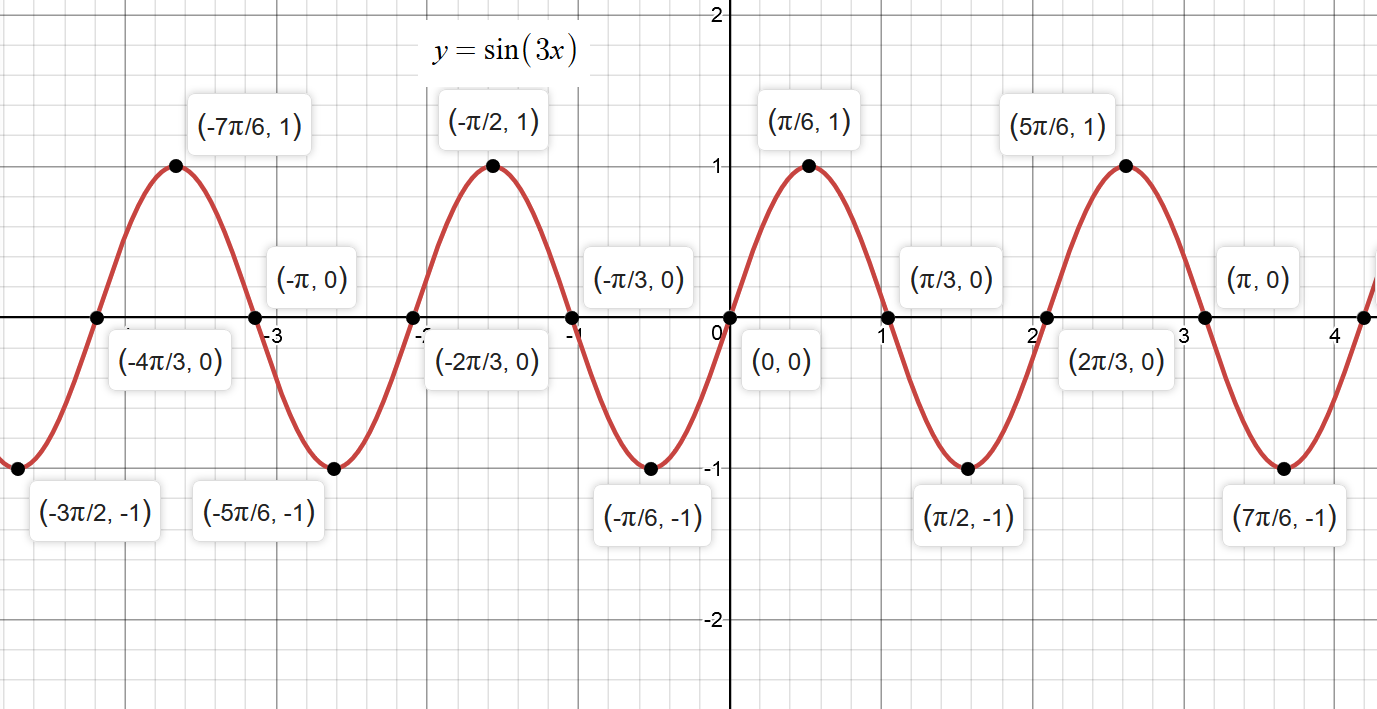
How Do You Graph Y Sin3x Socratic

How To Graph Cosine Functions Y 2 Cos X P 2 1 Youtube

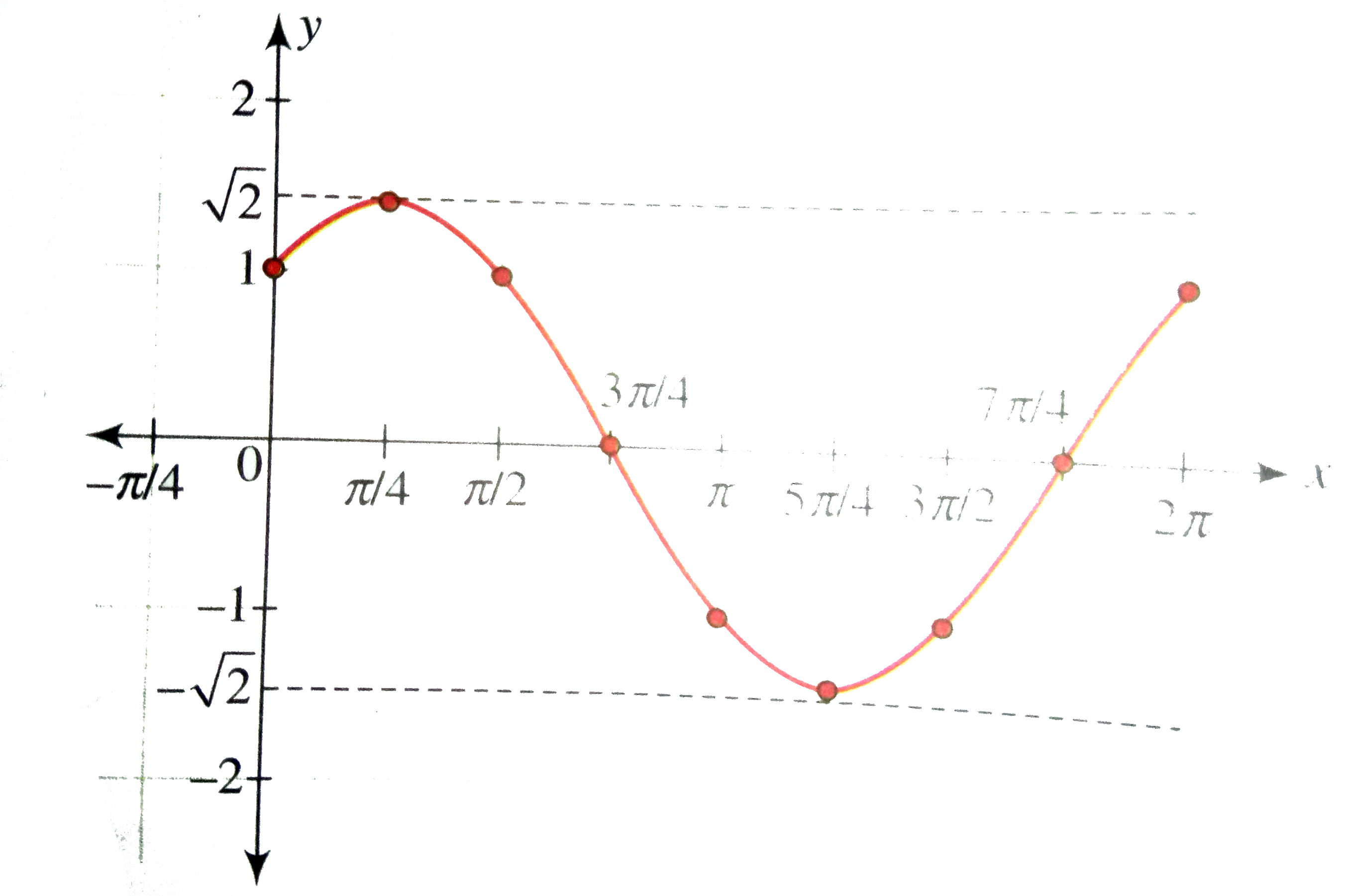
Draw The Graph Of Y Sin X Cos X X In 0 2pi

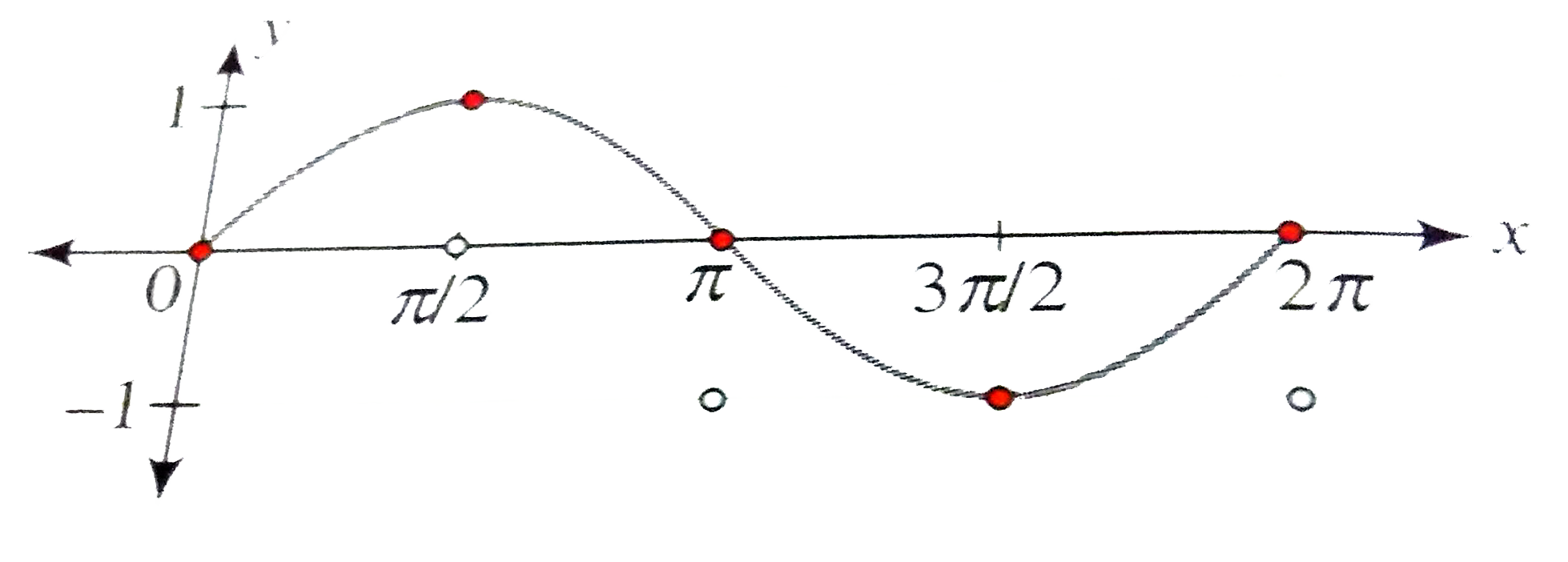
Draw The Graph Of Y Sin X X In 0 2pi Where Repre

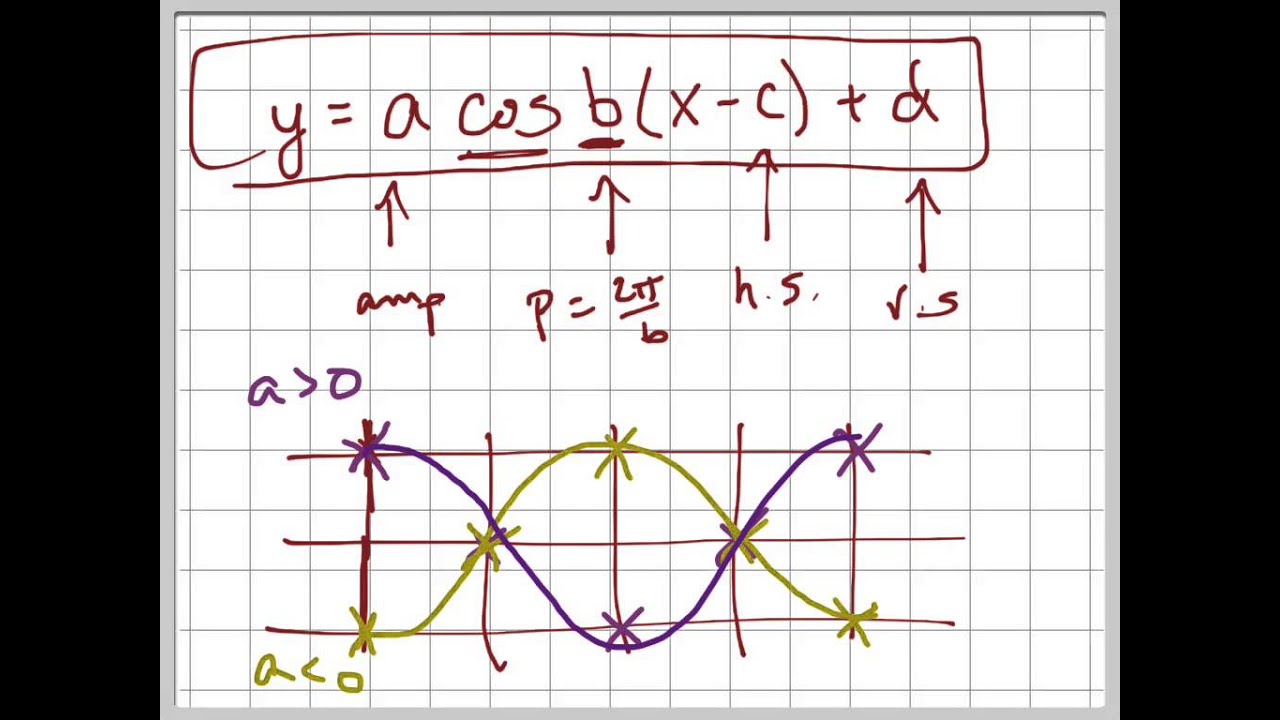
Graph Y 1 3 Cos X P 2 Youtube

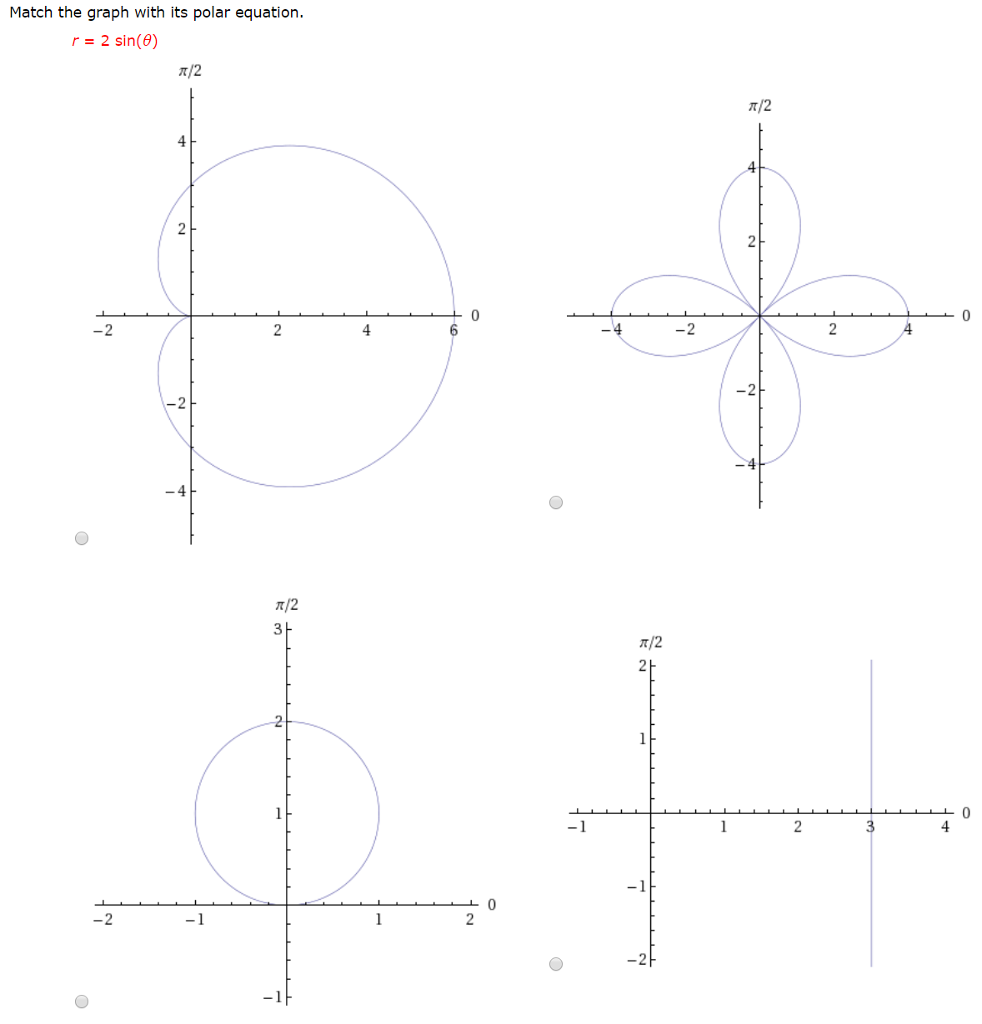
Solved Match The Graph With Its Polar Equation R 2 Sin Chegg Com

Steps For Graphing Tangent And Cotangent P

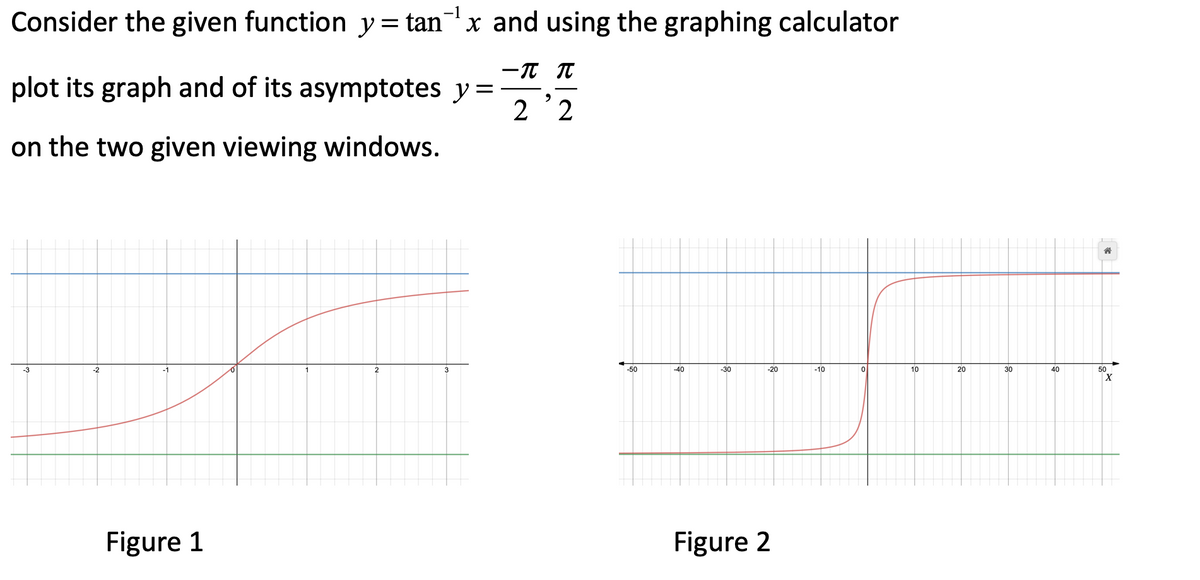
Answered Graph Y Tan 1 X And Its Two Bartleby

3 Day 1 Fdp Python 3

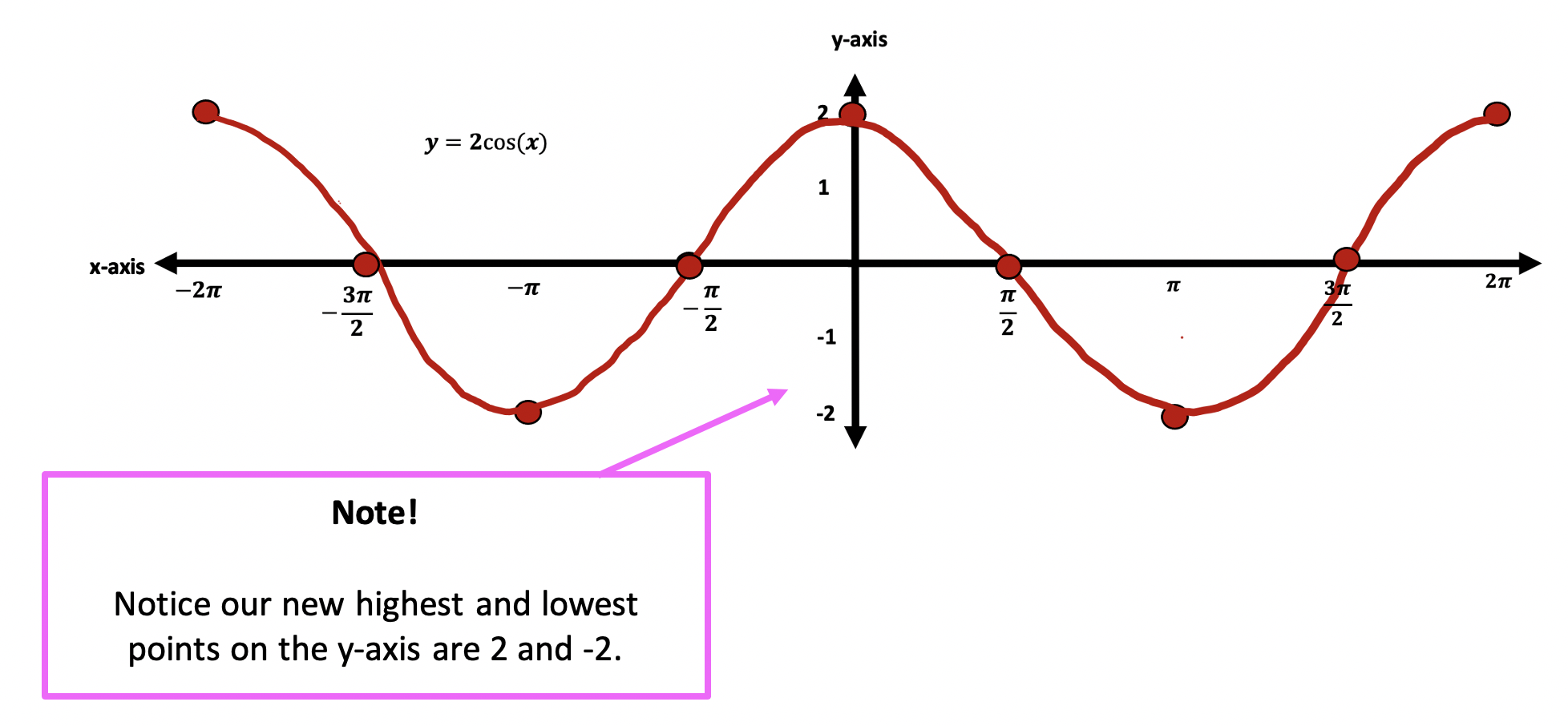
Trig Functions Amp Freq Phase Shifts Algebra 2 Trig Mathsux 2

Pcp L2 On The Axis Below Soundwaves And Trig Worksheet

Sine Graph Solutions Examples Videos

Polar Graphing Supposed Range Is Between 0 To Pi But Graph Drawn Range From Pi 2 To Pi 2 Mathematics Stack Exchange

Pplato Flap Phys 1 3 Graphs And Measurements

Pin On Math Videos

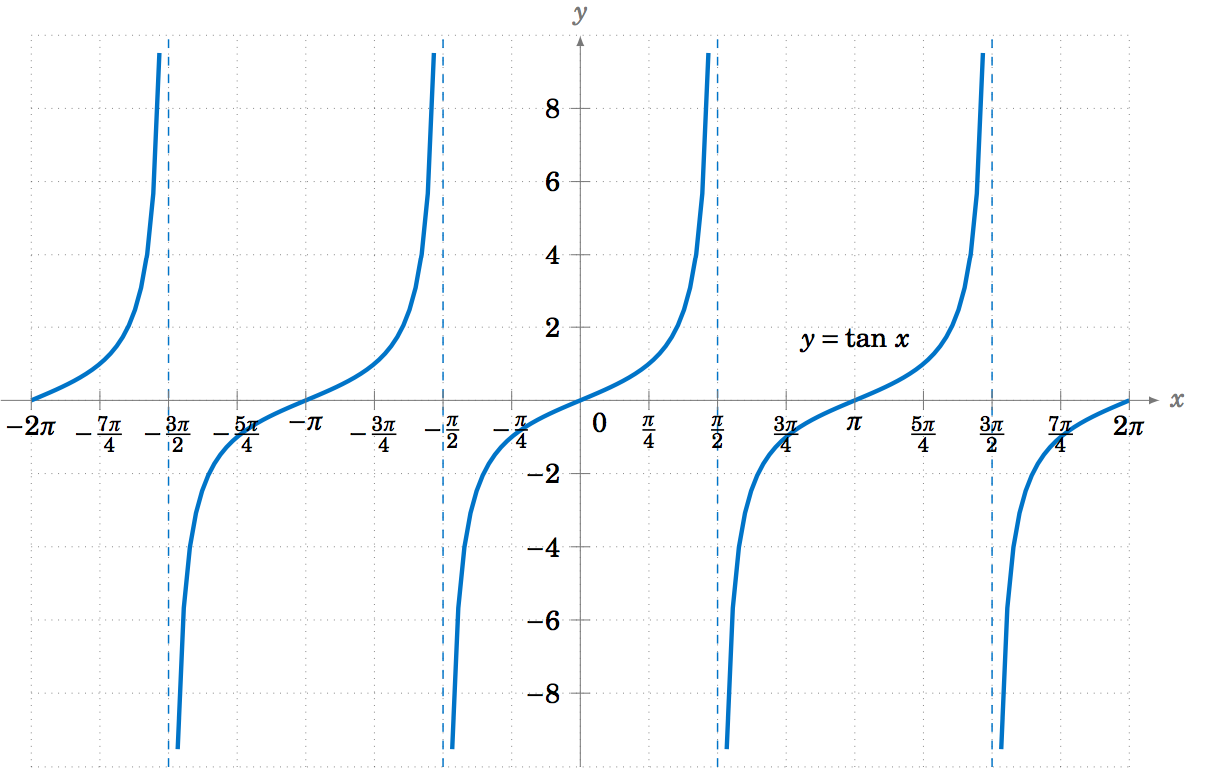
5 1 Graphing The Trigonometric Functions Mathematics Libretexts

Desmos Com Graph Only Goes From P 2 To P 2 Mathematics Stack Exchange

Graph Of Y Tan X Video Trigonometry Khan Academy

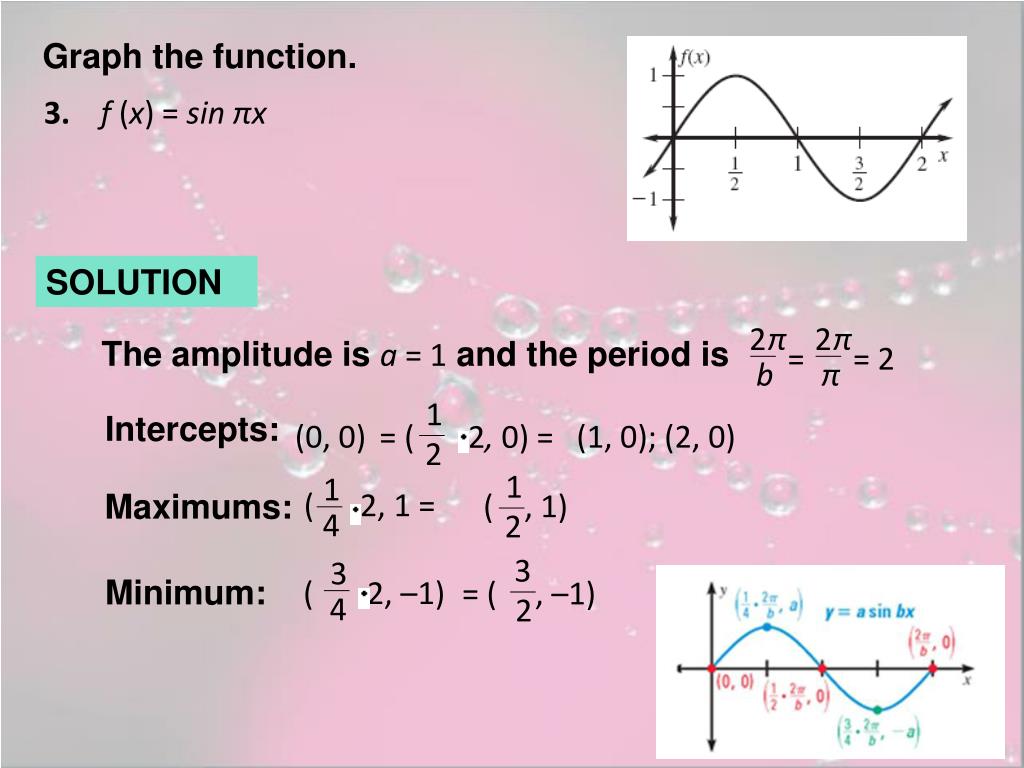
Ppt 10 1 Graph Sine Cosine And Tangent Functions Powerpoint Presentation Id

Webpage Of Dr Tom Cuchta

Drill For Exam Graph Cie

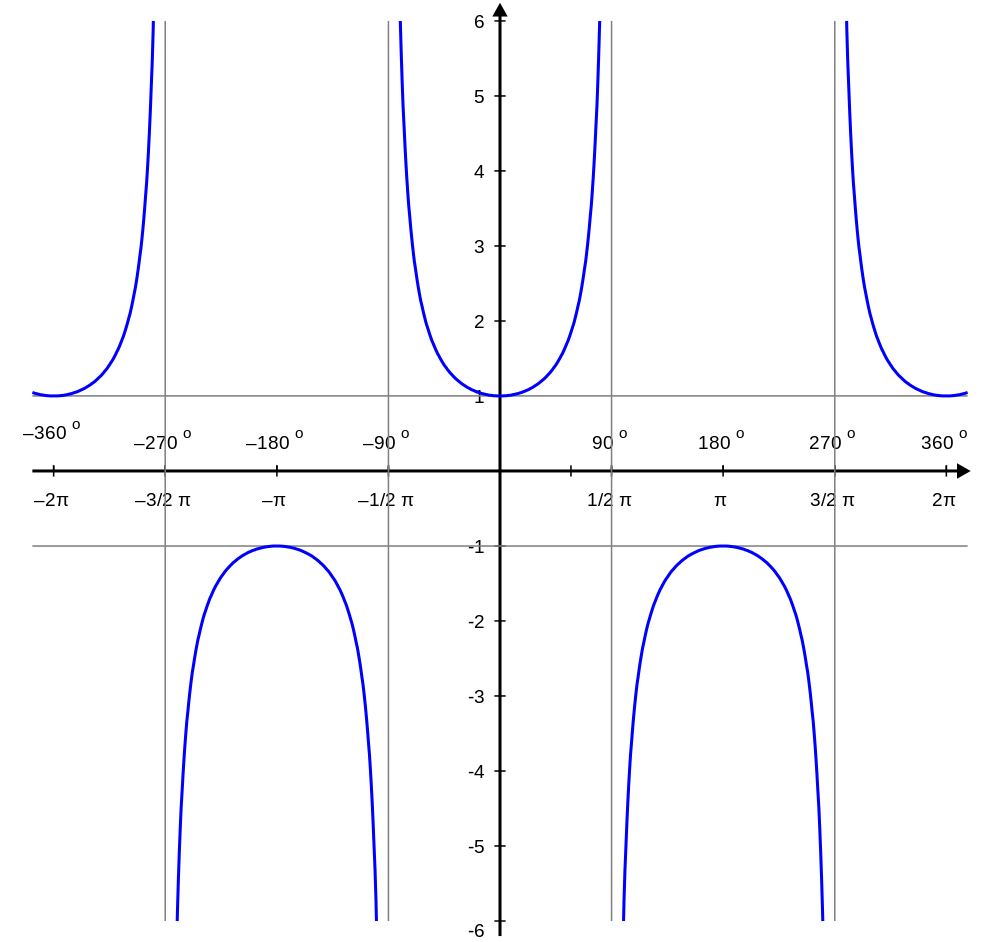
Secant Calculator

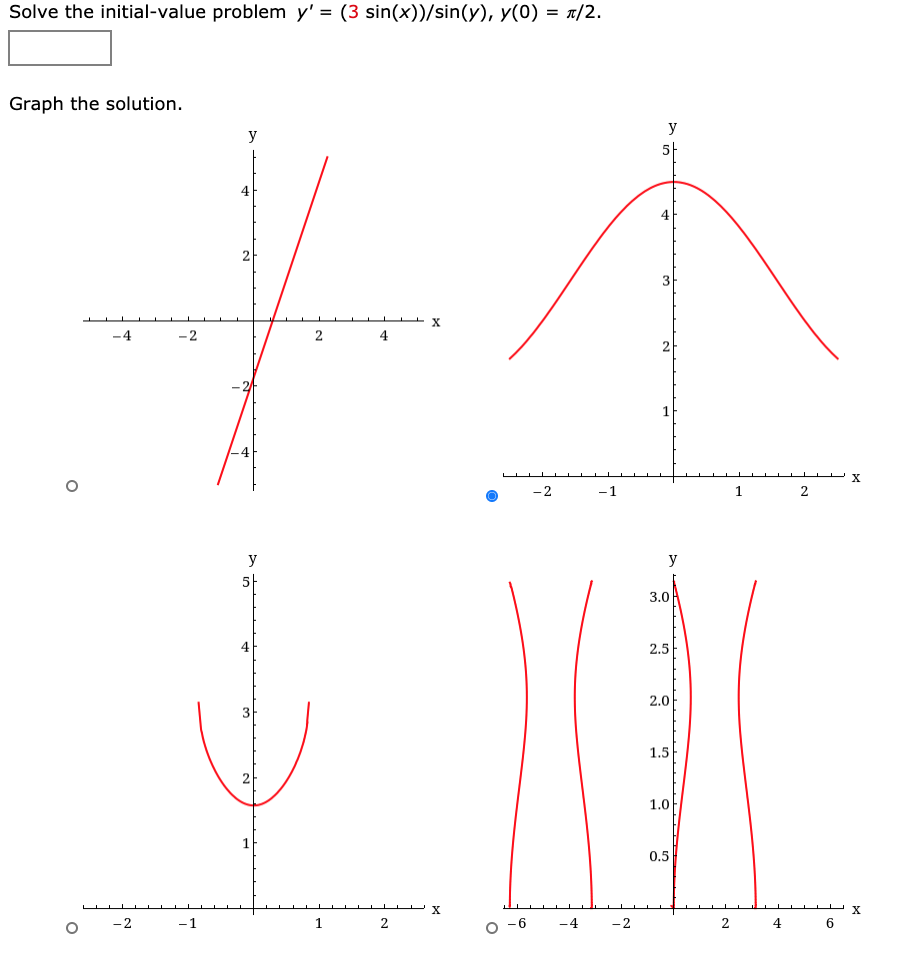
Solved Solve The Initial Value Problem Y 3 Sin X Si Chegg Com

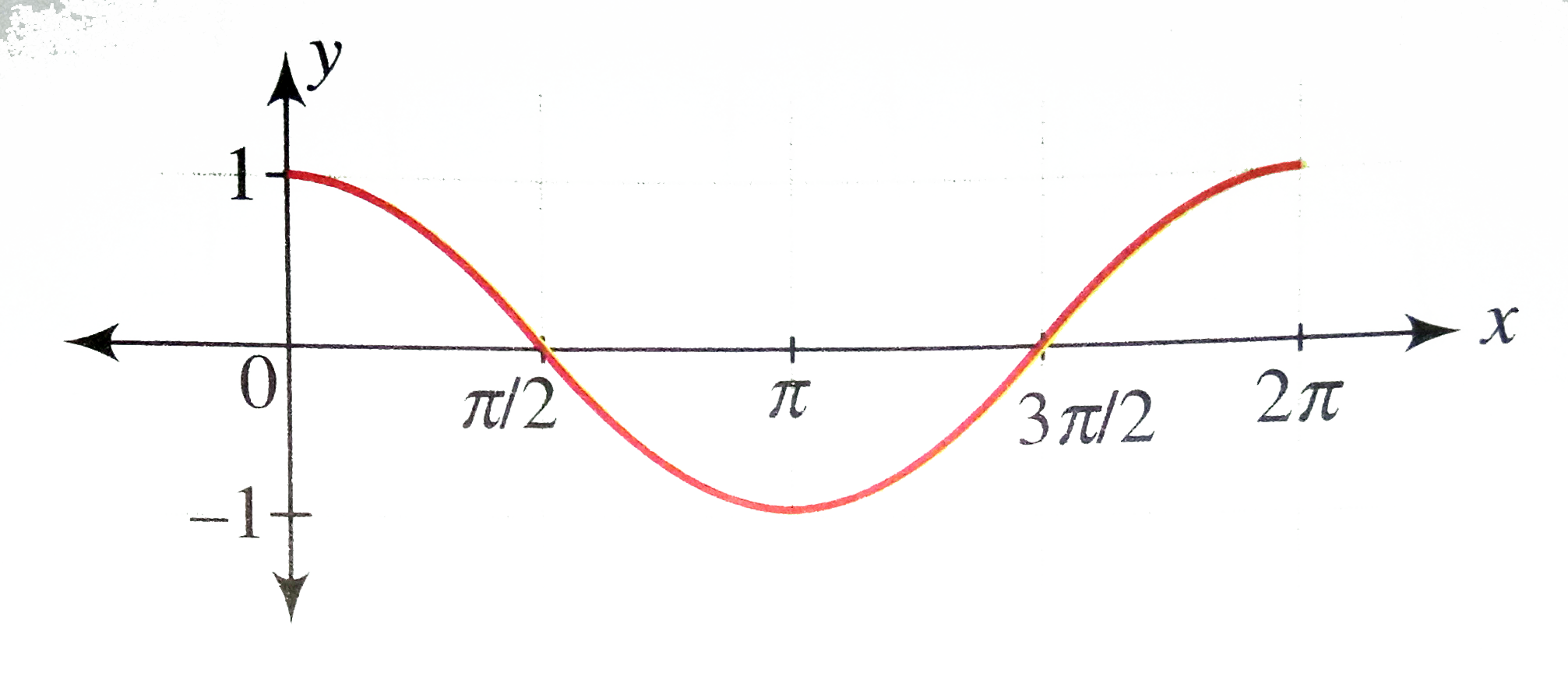
Draw The Graph Of Y Cos X X In 0 2pi Where Repres

Answer In Calculus For Jon Jay Mendoza

Chapter 22

Transforming Sinusoidal Graphs Vertical Horizontal Stretches Video Khan Academy

Let R Be The Region Between The Graphs Of Y 1 And Y Sinx From X 0 To X Pi 2 How Do You Find The Volume Of Region R Revolved About The X Axis Socratic

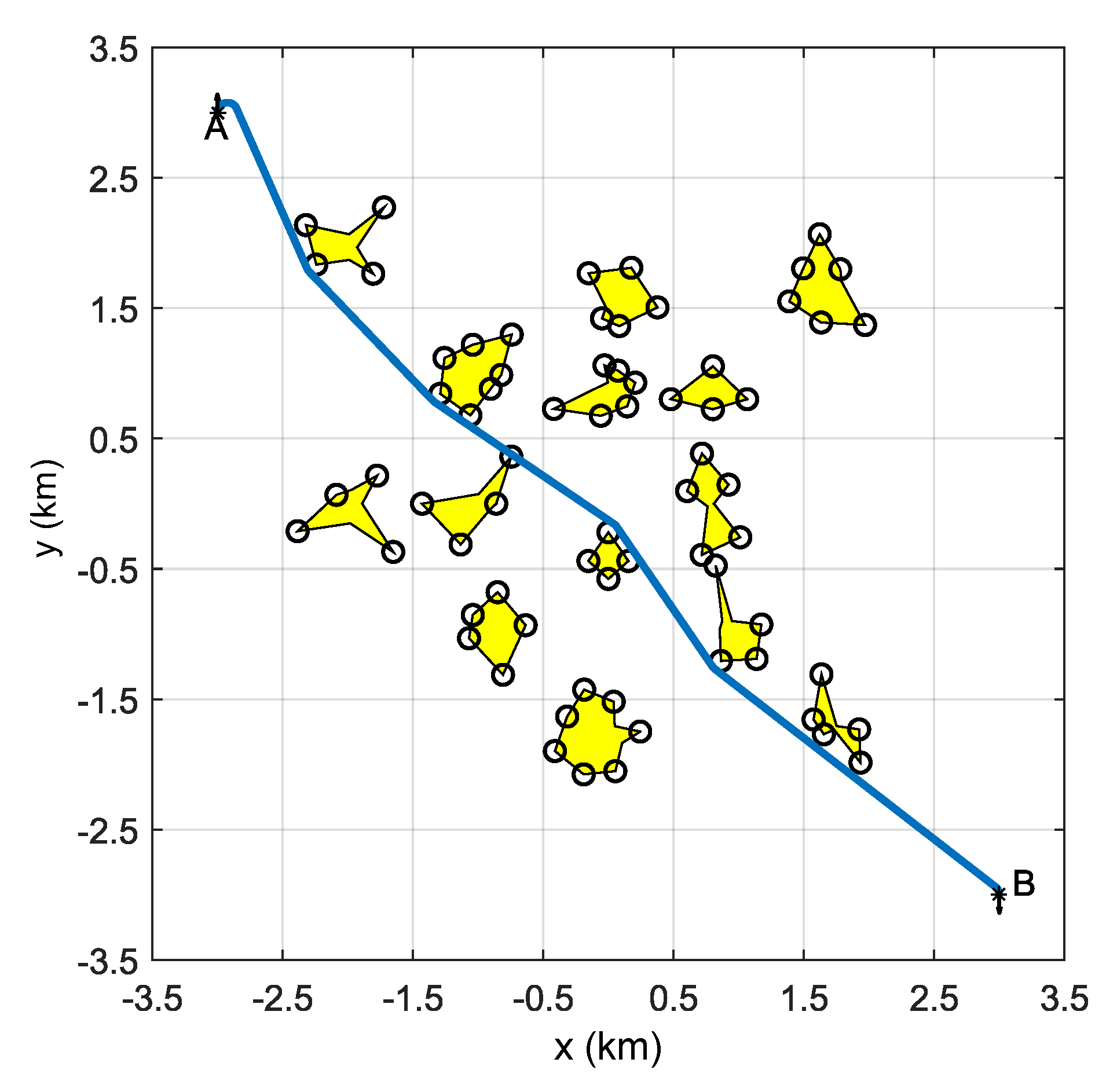
Applied Sciences Free Full Text Path Planning And Real Time Collision Avoidance Based On The Essential Visibility Graph Html

Quiz Worksheet How To Graph The Tangent Function Study Com